如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,DE是AB的中垂线.已知△ADC的面积是1.求

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/17 08:06:25

如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,DE是AB的中垂线.已知△ADC的面积是1.求
1.∠B的度数 2.△ABC的面积

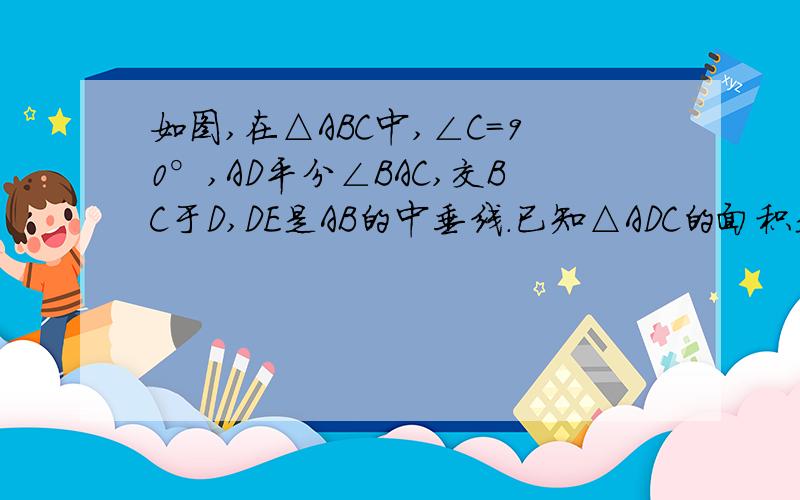
在△ABC中∵AD平分∠BAC
∴∠CAD=∠DAE(角平分线的定义）
∵DE是AB的中垂线
∴AD=BD（线段垂直平分线上的点到线段两端距离相等）
∴∠DAE=∠B(等边对等角）
∴∠CAD=∠DAE=∠B（等量代换）
∵∠C=90°
∵∠CAD+∠DAE+∠B=180°－∠C=90°
∴∠B=30°
（2）∵DC⊥AC DE⊥AB
∵AD平分∠BAC ∴∠CAD=∠DAE
∴DE=DE（角平分线上的点到角的两边距离相等）
∵AD=AD（公共边）
∴△ACD≌△AED（（AAS）
∴S△ACD=S△AED=1
∵AE=BE DE=DE（公共边） ∠AED=∠BED=90°
∴△ADE≌△BDE（SAS）
∴S△ADE=S△BDE=1
∴S.△ABC=3

如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,DE是AB的中垂线.已知△ADC的面积是1.求如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,DE是AB的中垂线.已知△ADC的面积为1.求：如图,在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,DE是AB的中垂线已知△ADC的面积为1,求：如图已知在三角形ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E,求证DE^2=BE×CE 如图,已知在△abc中AD平分∠BAC EM是AD的中垂线交BD延长线于E,求证DE²=BE×CE 如图,△ABC中,AD平分∠BAC,DE是BC的中垂线,E为垂足；过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是5cm，如图,在△ABC中,∠C=90°,CM⊥AB于M,AD平分∠BAC交CM于D,交BC于T,过D作DE∥AB交BC于E,求如图,在△ABC中,∠C＝90°,AC＝BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是5Cm, 已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,AB=18.求△ 如图,△ABC中,AD平分∠BAC,DE是BC的中垂线,E为垂足；过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,A 如图△ABC中,AD平分∠BAC,DE是BC的中垂线,E为垂足；过D作DM⊥AB于M,DN⊥AC交AC的延长线于N,求证