已知f(x)=sinx•cosx+sin2x.
来源:学生作业帮 编辑:神马作文网作业帮 分类:综合作业 时间:2024/11/18 13:09:52
已知f(x)=sinx•cosx+sin2x.
(1)求f(x)的最小正周期和单调递增区间;
(2)若f(x)的图象关于直线x=x0对称,且-1<x0<0,求x0的值.
(1)求f(x)的最小正周期和单调递增区间;
(2)若f(x)的图象关于直线x=x0对称,且-1<x0<0,求x0的值.
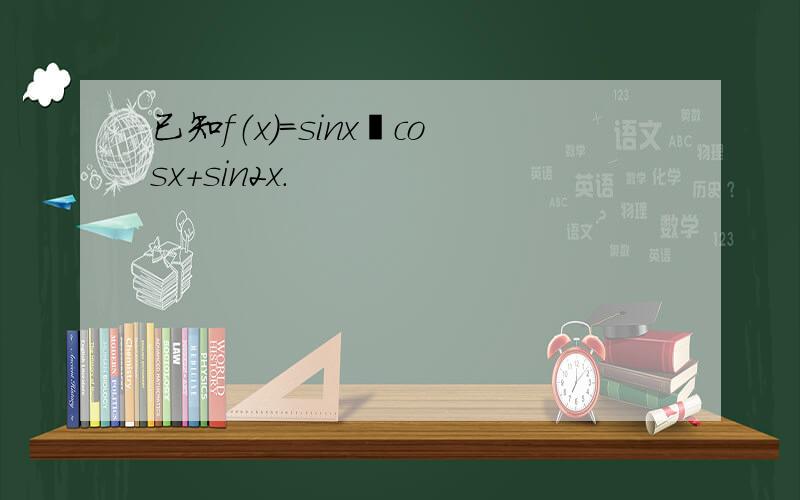
f(x)=sinx•cosx+sin2x=
1
2sin2x+
1
2(1−cos2x)=
2
2sin(2x−
π
4)+
1
2
(1)∴最小正周期为T=
2π
2=π,由2kπ−
π
2≤2x−
π
4≤2kπ+
π
2 k∈Z,
得x∈[kπ−
π
8,kπ+
3π
8] k∈Z,
∴f(x)的单调增区间是[kπ−
π
8,kπ+
3π
8] k∈Z.
(2)由题意:2x0−
π
4=kπ+
π
2,得x0=
1
2kπ+
3π
8 k∈Z,
∵-1<x0<0,即−1<
1
2kπ+
3π
8<0 k∈Z,
当k=-1时,x0=−
π
8.
1
2sin2x+
1
2(1−cos2x)=
2
2sin(2x−
π
4)+
1
2
(1)∴最小正周期为T=
2π
2=π,由2kπ−
π
2≤2x−
π
4≤2kπ+
π
2 k∈Z,
得x∈[kπ−
π
8,kπ+
3π
8] k∈Z,
∴f(x)的单调增区间是[kπ−
π
8,kπ+
3π
8] k∈Z.
(2)由题意:2x0−
π
4=kπ+
π
2,得x0=
1
2kπ+
3π
8 k∈Z,
∵-1<x0<0,即−1<
1
2kπ+
3π
8<0 k∈Z,
当k=-1时,x0=−
π
8.
已知函数f(x)=sinx•cosx+sin2x(x∈R).
已知函数f(x)=sin2x(sinx+cosx)/cosx
已知函数f(X)=(sinx-cosx)sin2x/sinx.
已知函数y=f(x)=sin2x+sinx•cosx+cos2x
(2014•长沙二模)已知函数f(x)=(sinx+cosx)2+23sin2x.
已知f(x)=(sinx+cosx)²/2+2sin2x-cos²2x
已知函数f(x)=[(2根号3sin^2x-sin2x)*cosx/sinx]+1
已知函数f(x)=23sinx•cosx+cos2x-sin2x-1(x∈R)
已知函数F(x)=(sinx一cosx)sin2x/sinx求f(x)定义域
已知函数f(x)=(sinx-cosx)sin2x/sinx,求f(x)单调减区间
已知函数f(x)=3sinx•cosx+sin2x.
已知函数f(x)=2cosx•sin(x+π3)−3sin2x+sinx•cosx.