在△ABC中AB=AC=6 BC=5 D是AB上一点 BD=2 e是BC上一动点 连接DE 并作角DEF=角B 射线EF
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/20 03:49:15
在△ABC中AB=AC=6 BC=5 D是AB上一点 BD=2 e是BC上一动点 连接DE 并作角DEF=角B 射线EF交线段AC于F
求;连接DF,如果△DEF与△DBE相似 求FC的长
先证明△BDE∽△CEF
∵∠B+∠DEB+∠BDE=180°
∠DEB+∠DEB+∠FEC=180°
又∵∠DEF=∠B
∴∠BDE=∠FEC
∵AB=AC
∴∠B=∠C
∴△BDE∽△CEF
若△DFE∽△DEB,
前面已经证得△DEB∽△EFC
∴∠BDE=∠EDF,∠DFE=∠CFE
∴点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线
又∵AB=AC
∴AE又是底边BC中点
∴BE=CE=5/2
△DEB∽△EFC
∴BD:EC=BE:CF
即2:(5/2)=(5/2):FC
∴FC=25/8
【点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线】
怎么得的?
应该要分类讨论△DFE∽△DEB或△FDE∽△DEB

求;连接DF,如果△DEF与△DBE相似 求FC的长
先证明△BDE∽△CEF
∵∠B+∠DEB+∠BDE=180°
∠DEB+∠DEB+∠FEC=180°
又∵∠DEF=∠B
∴∠BDE=∠FEC
∵AB=AC
∴∠B=∠C
∴△BDE∽△CEF
若△DFE∽△DEB,
前面已经证得△DEB∽△EFC
∴∠BDE=∠EDF,∠DFE=∠CFE
∴点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线
又∵AB=AC
∴AE又是底边BC中点
∴BE=CE=5/2
△DEB∽△EFC
∴BD:EC=BE:CF
即2:(5/2)=(5/2):FC
∴FC=25/8
【点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线】
怎么得的?
应该要分类讨论△DFE∽△DEB或△FDE∽△DEB

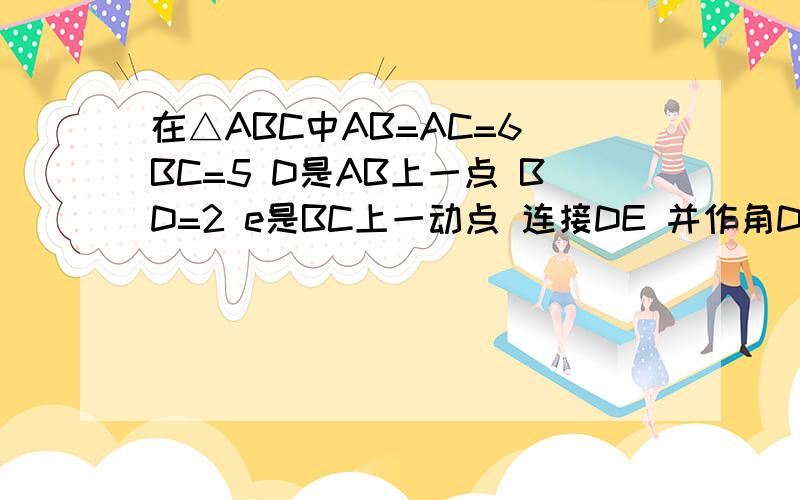
先证明△BDE∽△CEF
∵∠B+∠DEB+∠BDE=180°
∠DEB+∠DEB+∠FEC=180°
又∵∠DEF=∠B
∴∠BDE=∠FEC
∵AB=AC
∴∠B=∠C
∴△BDE∽△CEF
若△DFE∽△DEB,
前面已经证得△DEB∽△EFC
∴∠BDE=∠EDF,∠DFE=∠CFE
∴点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线
又∵AB=AC
∴AE又是底边BC中点
∴BE=CE=5/2
△DEB∽△EFC
∴BD:EC=BE:CF
即2:(5/2)=(5/2):FC
∴FC=25/8
【点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线】
怎么得的?
应该要分类讨论△DFE∽△DEB或△FDE∽△DEB
∵∠B+∠DEB+∠BDE=180°
∠DEB+∠DEB+∠FEC=180°
又∵∠DEF=∠B
∴∠BDE=∠FEC
∵AB=AC
∴∠B=∠C
∴△BDE∽△CEF
若△DFE∽△DEB,
前面已经证得△DEB∽△EFC
∴∠BDE=∠EDF,∠DFE=∠CFE
∴点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线
又∵AB=AC
∴AE又是底边BC中点
∴BE=CE=5/2
△DEB∽△EFC
∴BD:EC=BE:CF
即2:(5/2)=(5/2):FC
∴FC=25/8
【点E是DE,EF两角平分线交点
连接AE,则AE是∠BAC的平分线】
怎么得的?
应该要分类讨论△DFE∽△DEB或△FDE∽△DEB
在△ABC中AB=AC=6 BC=5 D是AB上一点 BD=2 e是BC上一动点 连接DE 并作角DEF=角B 射线EF
如图,已知在△ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,连接DE,作∠DEF=∠C
如图,已知△ABC中,AB=AC=6,BC=5,D是AB边上一点,BD=2,E是BC上一动点,联结DE,并作∠DEF=∠
如图,已知△ABC中,AB=AC=6,BC=5,D是AB边上一点,BD=2,E是BC边上一动点,联结DE,联结DE,并作
在三角形ABC中AB=AC,D、E分别是AB、BC上的点连接DE并延长交AC延长线于点F,若DE=EF,求证:BD=CE
△ABC中,AB=AC,D,E分别是AB和BC上的点,连接DE并延长交AC的延长线于F,若DE=EF,求证BD=CF
已知,如图,在△ABC中,点D,E在BC上,且CD=DE,过点E作EF平行于AB交AD于F,且EF=AC,求证AD是角B
如图,三角形ABC中,D在AB上,E在AC上,G在BC上.连接DE,DG,F是DG上一点,连接EF.已知角1+角2=18
在△ABC中,∠A=90度,AB=AC,AM⊥BC,与M,点D为射线AB上一点,点E为射线AC上一点,BD=CE,连接D
如图所示,在△ABC中,∠CBA=90°,D是AB延长线上的一点,E在BC上,连接DE并延长交AC于点F,EF=FC,求
如图,在△ABC中,AB=AC,D为AB上一点,F是AC延长线上一点,且BD=CF,连接DF交BC于点E,求证:DE=E
已知三角形ABC中,AB=AC,D.E分别是AB和BC上的点,连接DE并延长与AC的延长线交于点F,若DE=EF,证明B