xf(x)-f(x)=xe^x
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/08 08:47:10
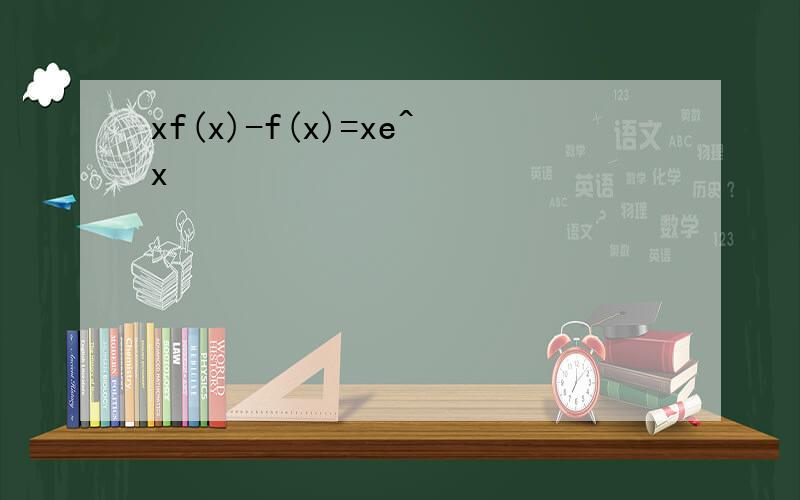
凑一下就可以,因为df(x^2)=2xf'(x^2)所以∫xf(x^2)f'(x^2)dx=1/2∫[2xf'(x^2)]*f(x^2)dx=1/2∫f(x^2)df(x^2)=1/2*1/2*[f(
答案:[f^2(x^2)]/4提示:∫xf(x^2)f'(x^2)dx=1/2∫f(x^2)f'(x^2)dx^2,然后令下x^2=t即可
对已知式求导得f'(x)=2x+xf(x),设y=f(x),则y'=x(2+y),dy/(y+2)=xdx,∴ln(y+2)=x^2/2+c1,∴y+2=ce^(x^2/2),∴y=f(x)=ce^(
∫[f(x)+xf'(x)]dx=∫f(x)dx+∫xf'(x)dx=∫f(x)dx+∫xdf(x)=∫f(x)dx+xf(x)-∫f(x)dx=xf(x)+C.
你要明白一点就行了,那就是积分符号1到0,xf(x)dx是个常数.我们可以把它设为C.然后得出f(x)=x+C.然后得出xf(x)的表达式.你把这个表达式积分得出c的等式.解出C.然后不就出来了.
积分与微分(求导)是互逆运算,所以xf(x)的积分再进行微分(求导)还是xf(X),微分就是求导,两边同时进行求导,自然得出结论再问:那是不是xf(x)换成其他随便什么,结果还是原来?再答:通常是的
∫(0->1)xf(t)dt=f(x)+xe^xf(x)=-xe^x+∫(0->1)xf(t)dt(1)∫(0->1)f(x)dx=∫(0->1)[-xe^x+∫(0->1)xf(t)dt]dx=∫(
letxe^(x^2)=∫f(x)dxe^(x^2).[1+2x^2]=f(x)∫xf'(x)dx=∫xdf(x)=xf(x)-∫f(x)dx=xf(x)-xe^(x^2)+C=xe^(x^2).[1
已知xe^x为f(x)的一个原函数,那么f(x)=d(xe^x)/dx=(x+1)e^xf(x)导=(x+2)e^x原式=∫(0,1)x(x+2)e^xdx=∫(0,1)(x^2+2x)e^xdx分部
[f(x)+xf'(x)]dx=f(x)dx+xdf(x)=f(x)dx+xf(x)-f(x)dx=xf(x)+c(分布积分法)
f(x)=xe^kxf'(x)=x'*e^kx+x*(e^kx)'=e^kx+kx*e^kx=(1+kx)e^kx
喜欢这个ID号,答一下.根据题意,g(x),f(x)关于x=1对称,则有:g(1+x)=f(1-x)令x=x-1,则有g(x)=f(2-x)=(2-x)e^(-(2-x))=(2-x)e^(x-2):
挺好的题f(xy)=xf(y)+yf(x)---(1)设y=c=常量则:f(cx)=cf(x)+f(c)x两边求导数f'(cx)*c=cf'(x)+f(c)cf'(cx)-cf'(x)=f(c)此式对
(1)fˊ(x)=e^x+xe^xf`(0)=1f(0)=1切线方程为y=x+1(2)fˊ(x)=e^x+xe^x=e^x(1+x)因为e^x>0,故1+x0,f(x)为增函数.(-∞,-1)上单调递
f(x)'=e^(-x)-xe^(-x)=e^(-x)(1-x)这样当x在[0,1]上时f递增,在[1,2]上f递减又f(0)=0,f(1)=e^(-1),f(2)=2e^(-2)因此最大值为e^(-
f'(x)=(0.5x^2+e^x-xe^x)'=x+e^x-e^x-xe^x=x-xe^x导数等于0时,x等于0请注意最后一项的求导结果(应用乘积函数的求导法则)(F(x)G(x))'=F(x)G'
既然xe^x是原函数,那么直接将xe^x微分得到f(x)=(1+x)e^x,带入积分得∫xf(x)dx=∫x(1+x)e^xdx,利用分部积分,分成x(1+x)和e^x,∫x(1+x)e^xdx=x(
题目是不是有错,第二个表达式,你确定是这样?再问:是g(x)=xe^x再答: