(2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=12AA1,∠ACB=90°,G为BB1的中点.
来源:学生作业帮 编辑:神马作文网作业帮 分类:综合作业 时间:2024/11/12 23:25:52
 (2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=
(2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=| 1 |
| 2 |
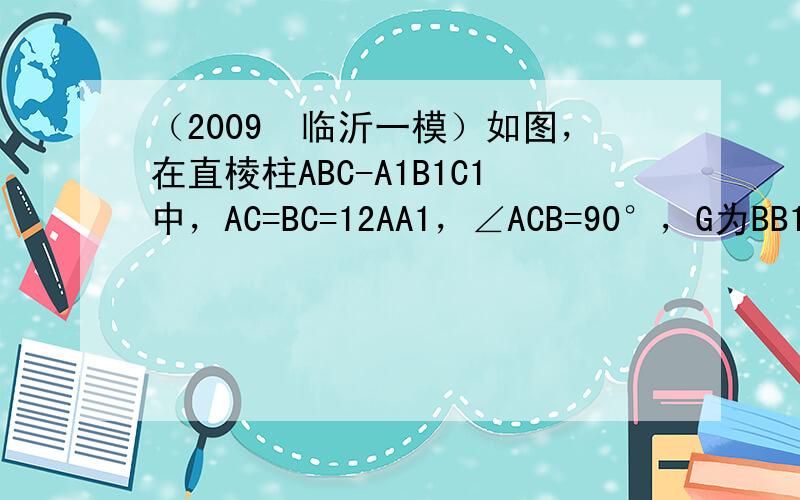
 (I)证明:在直棱柱ABC-A1B1C1中,有A1C1⊥CC1.
(I)证明:在直棱柱ABC-A1B1C1中,有A1C1⊥CC1.∵∠ACB=90°,∴A1C1⊥C1B1,即A1C1⊥平面C1CBB1,
∵CG⊂平面C1CBB1,∴A1C1⊥CG.┉┉┉┉┉┉┉┉(2分)
在矩形C1CBB1中,CC1=BB1=2BC,G为BB1的中点,
CG=
2BC,C1G=
2BC,CC1=2BC
∴∠CGC1=90,即CG⊥C1G┉┉┉┉┉┉┉┉(4分)
而A1C1∩C1G=C1,
∴CG⊥平面A1GC1.
∴平面A1CG⊥平面A1GC1.┉┉┉┉┉┉┉┉(6分)
(II)(法一)由于CC1平面ABC,∠ACB=90°,建立如图所示的空间坐标系,设AC=BC=
1
2CC=a,则A(a,0,0),B(0,a,0)A1(a,0,2a),G(0,a,a).
∴
CA=(a,0,2a),
CG=(0,a,a).┉┉┉┉┉┉┉┉(8分)

设平面A1CG的法向量n1=(x1,y1,z1),
由
CG•n1=0
CA1•n1=0得
ax1+2az1=0
ay1+az1=0
令z1=1,n1=(-2,-1,1).┉┉┉┉┉┉┉┉(9分)
又平面ABC的法向量为n2=(0,0,1)┉┉┉┉┉┉┉┉(10分)
设平面ABC与平面A1CG所成锐二面角的平面角为θ,
则cosθ=|
n1•n2
|n1||n2||=
1
6=
6
6┉┉┉┉┉┉┉┉(11分)
即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为
6
6.┉┉┉(12分)
(法二)延长A1G、AB相交于P,过A作AF⊥PC交PC延长线于点F,连接A1F
∵AA1⊥平面ABC,AF⊥PC,∴A1F⊥PF
∴∠AFA1为平面ABC与平面A1CG所成二面角的平面角.┉┉┉┉┉┉┉┉(8分)
由(I)知CG⊥A1G,∴△PGC~△PFA1,
设AC=BC=a,∴CG=
2a,A1G=GP=
3a,CP=
5a
由
CG
A1F=
CP
A1P,
得A1F=
CG.A1P
CP=
2a•2
3a
5=
2
30a
5┉┉┉┉┉┉┉┉┉┉(10分)AF=
A1F2−A1A2=
24
5a2−4a2=
2
5
5a.
∴cos∠AFA1=
AF
A1F=
2
5
5a
2
30
5a=
6
6.┉┉┉┉┉(12分)
(2009•临沂一模)如图,在直棱柱ABC-A1B1C1中,AC=BC=12AA1,∠ACB=90°,G为BB1的中点.
(2006•南汇区二模)如图,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为BB1的中点
一道数学立体几何题.在直棱柱ABC-A1B1C1中,AC=BC=1/2(AA1),角ACB等于90度,G为BB1的中点.
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为BB1的中点,D点在AB上且DE=3
(2014•河南模拟)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E,F,G分别是AA1,AC,BB1的中
如图,在直三棱柱ABC=A1B1C1中,∠ACB=90°,E,F,D分别是AA1,AC,BB1的中点,且CD⊥C1D.
如图,在直三棱柱ABC=A1B1C1中,∠ACB=90°,E,F,D分别是AA1,AC,BB1的中点,且CD⊥C1D.(
直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,点D在AB上,且DE=根号3
(2014•贵州二模)已知直三棱柱ABC-A1B1C1中,∠ACB=π2.AC=CB=AA1=2,E为BB1的中点,D在
直棱柱ABC-A1B1C1中,AC=BC=根号3,AA1=2,∠ACB=90°,M、N分别为AA1、BC1的中点.
如图,直三棱柱ABC-A1B1C1中,AC=BC=1,∠ACB=90°,AA1=2,D 是A1B1中点.
(2014•重庆二模)如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB中点,