如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，DE⊥面CBB1．

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/11 19:00:06

如图，AA₁、BB₁为圆柱OO₁的母线，BC是底面圆O的直径，D、E分别是AA₁、CB₁的中点，DE⊥面CBB₁．

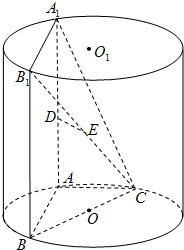
（1）证明：DE∥面ABC；
（2）求四棱锥C-ABB₁A₁与圆柱OO₁的体积比；
（3）若BB₁=BC，求CA₁与面BB₁C所成角的正弦值．

如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，DE⊥面CBB1．

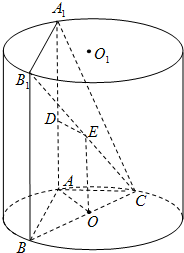（1）证明：连接EO，OA．∵E，O分别为B₁C，BC的中点，∴EO∥BB₁．
又DA∥BB₁，且DA=EO=
1
2BB1．∴四边形AOED是平行四边形，
即DE∥OA，DE⊄面ABC．∴DE∥面ABC．
（2）由题DE⊥面CBB₁，且由（1）知DE∥OA．∴AO⊥面CBB₁，∴AO⊥BC，
∴AC=AB．因BC是底面圆O的直径，得CA⊥AB，且AA₁⊥CA，
∴CA⊥面AA₁B₁B，即CA为四棱锥的高．
设圆柱高为h，底半径为r，则V_柱=πr²h，V锥=
1
3h(
2r)•(
2r)=
2
3hr2，
∴V_锥：V_柱=
2
3π．
（3）作过C的母线CC₁，连接B₁C₁，则B₁C₁是上底面圆O₁的直径，

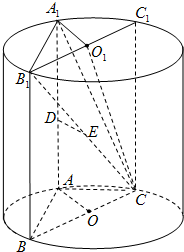
连接A₁O₁，得A₁O₁∥AO，又AO⊥面CBB₁C₁，
∴A₁O₁⊥面CBB₁C₁，连接CO₁，
则∠A₁CO₁为CA₁与面BB₁C所成的角，
设BB₁=BC=2，则A1C=
22+(
2)2=
6，
A₁O₁=1．（12分）
在Rt△A₁O₁C中，sin∠A1CO1=
A1O1
A1C=

6
6．

如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，DE⊥面CBB1．圆柱OO1的高等于4cm,侧面积为16Pi平方厘米,AA1,BB1是它的两条母线,它们之间的距离是2根号3cm,M是BB 俺看不懂如图,在三棱柱ABC-A1B1C1中,BB1⊥面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点．若如图,直三棱柱ABC–A1B1C1中,D,E分别是AB,BB1的中点(1)证明BC1//平面A1CD(2)设AA1=AC 如图：直三棱柱ABC-A1B1C1中，AC=BC=AA1=2，∠ACB=90°．E为BB1的中点，D点在AB上且DE=3 高中立体几何题求解如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、CD的中点．设AA1=2，求三棱锥E- 如图，在直三棱柱ABC=A1B1C1中，∠ACB=90°，E，F，D分别是AA1，AC，BB1的中点，且CD⊥C1D．如图，在直三棱柱ABC=A1B1C1中，∠ACB=90°，E，F，D分别是AA1，AC，BB1的中点，且CD⊥C1D．（如图, 在正方体ABCD—A1B1C1D1中,E、F分别是CC1、AA1的中点．AA1=2. 如图，在正方体ABCD-A1B1C1D1中，E，F分别是棱AA1，BB1的中点，求异面直线A1F与D1E所成角的余弦值．（平面与平面性质）如图,四棱柱ABCD-A1B1C1D1中底面ABCD为正方形侧棱AA1⊥底面ABCD,E是棱BC的中点如图：直三菱柱ABC—A1B1C1中,AC=BC=AA1=2,角ACB=90度,E为BB1的中点,D点在AB上且DE=√