（2007•绵阳）如图，已知抛物线y=ax2+bx-3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心

来源：学生作业帮编辑：神马作文网作业帮分类：综合作业时间：2024/11/10 22:13:31

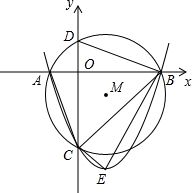（2007•绵阳）如图，已知抛物线y=ax²+bx-3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为

（2007•绵阳）如图，已知抛物线y=ax2+bx-3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心

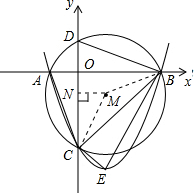（1）由题意可知C（0，-3），-
b
2a=1，
∴抛物线的解析式为y=ax²-2ax-3（a＞0），
过M作MN⊥y轴于N，连接CM，则MN=1，CM=
5，
∴CN=2，于是m=-1．
同理可求得B（3，0），
∴a×3²-2a×3-3=0，得a=1．
∴抛物线的解析式为y=x²-2x-3．

（2）由（1）得A（-1，0），E（1，-4），B（3，0），C（0，-3）．
∵M到AB，CD的距离相等，OB=OC，
∴OA=OD，
∴点D的坐标为（0，1），
∴在Rt△BCO中，BC=
OB2+OC2=3
2，
∴
OB
OD＝
3
1＝3，
在△BCE中，∵BC²+CE²=（3²+3²）+[（1-0）²+（-4+3）²]=20=（3-1）²+（0+4）²=BE²∴△BCE是Rt△

BC
CE＝
3
2

2＝3，
∴
OB
OD＝
BC
CE，
即
OB
BC＝
OD
CE，
∴Rt△BOD∽Rt△BCE，得∠CBE=∠OBD=β，
因此sin（α-β）=sin（∠DBC-∠OBD）=sin∠OBC=
CO
BC＝