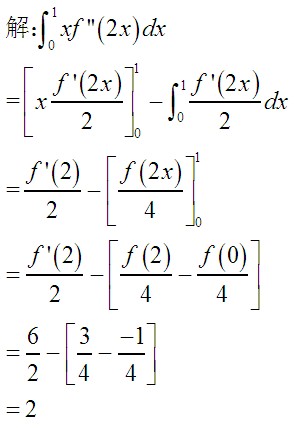高数定积分题：已知f(0)=-1 f(2)=3 f'(2)=6 求 ∫xf''(2x)dx 在［0,1］

高数定积分题：已知f(0)=-1 f(2)=3 f'(2)=6 求 ∫xf''(2x)dx 在［0,1］ f"(x)在[0,1]上连续,f'(1)=0,f(1)-f(0)=2,∫(0~1)xf"(x)dx=?(定积分) 设f(0)=1.f(2)=3,f`(2)=5,求 ∫(0~1)xf``(2x)dx.积分里面是两撇哦, 定积分∫(范围1-2)xf(x)dx=2,求定积分∫(范围0-3)f√(x+1)dx=? 定积分，f(x)=∫(1,x^2)e^-t^2dt,求 ∫(0,1)xf(x)dx f(x)=x+积分符号1到0,xf（x)dx,求f(x) 设f''(x)在[0,1]连续,且f(0)=1,f(2)=3,f'(2)=5,求∫[0,1]xf''(2x)dx 已知f(0)=1,f(2)=3,f(2)'=5.则积分xf(x)''dx上限为2,下限为0等于多少 已知f(x)具有二阶连续导数,且f(0)=1,f(2)=4,f'(2)=2 求∫xf''(2x)dx 已知f''(x)在[0,1]上连续,f'(1)=0,且f(1)-f(0)=2,则∫(0,1)xf''(x)dx= 已知f(0)=1,f(2)=3,f'(2)=5,求∫xf''(2x)dx{∫上面为1,下面为0} 已知f(x)=x^2+∫xf(x)dx求f(x)