探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥CD于点E．若AE=10，求四边形ABC

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/17 13:59:37

探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥CD于点E．若AE=10，求四边形ABCD的面积．
应用：如图②，在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，AE⊥BC于点E．若AE=19，BC=10，CD=6，则四边形ABCD的面积为______．

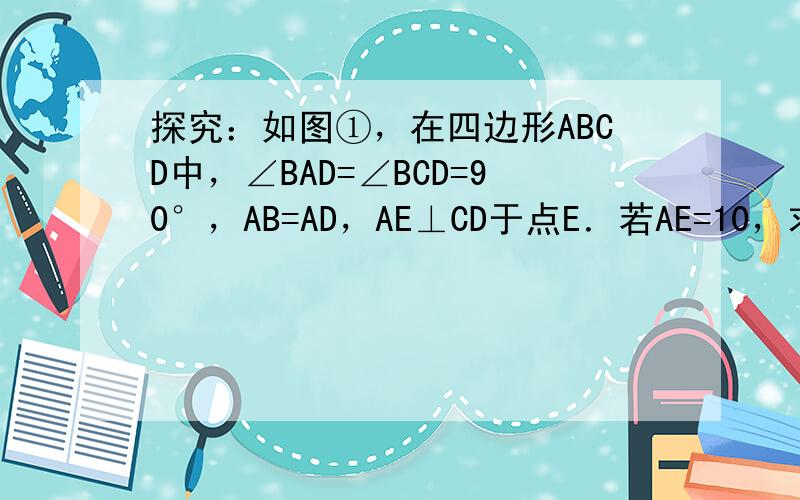
探究：如图①，过点A作AF⊥CB，交CB的延长线于点F，
∵AE⊥CD，∠BCD=90°，
∴四边形AFCE为矩形，
∴∠FAE=90°，
∴∠FAB+∠BAE=90°，
∵∠EAD+∠BAE=90°，
∴∠FAB=∠EAD，
∵在△AFB和△AED中，

∠FAB＝∠EAD
∠F＝∠AED＝90°
AB＝AD，

∴△AFB≌△AED（AAS），
∴AF=AE，
∴四边形AFCE为正方形，
∴S_{四边形ABCD}=S_{正方形AFCE}=AE²=10²=100；
应用：如图，过点A作AF⊥CD交CD的延长线于F，连接AC，
则∠ADF+∠ADC=180°，
∵∠ABC+∠ADC=180°，
∴∠ABC=∠ADF，
∵在△ABE和△ADF中，

∠ABC＝∠ADF
∠AEB＝∠F＝90°
AB＝AD，
∴△ABE≌△ADF（AAS），
∴AF=AE=19，
∴S_{四边形ABCD}=S_△ABC+S_△ACD
=
1
2BC•AE+
1
2CD•AF
=
1
2×10×19+
1
2×6×19
=95+57
=152．
故答案为：152．

探究：如图①，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥CD于点E．若AE=10，求四边形ABC 如图,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE垂直BC于点E,AE=2厘米,则四边形ABCD的面已知：如图，在四边形ABCD中，AD∥BC，AB=BC+AD，AE平分∠BAD交CD于点E．几何图形变换练习3如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=6,AE ⊥BC于E,AE=5,求四边如图,在凸四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB于点E,并且AE=二分之一(AB+AD) 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若AE=6,BE=2,求四边形ABED的面积如图,在四边形ABCD中,AD‖BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点.求证:四边形AE 已知,如图,在四边形ABCD中,∠BAD=∠C=90°且AB=AD,AE⊥BC垂足为E,若AE=2倍的根号3,求四边形面已知、如图,在四边形ABCD中,∠BAD=∠C=90°,且AB=AD,AE⊥BC垂足为E,若AE=2√3,求四边形的面积如图，四边形ABCD中，AB=AD，AC平分∠BCD，AE⊥BC，AF⊥CD．如图，在四边形ABCD中，AD∥BC，AE平分∠BAD交DC于点E，连接BE，且AE⊥BE，求证：AB=AD+BC．如图,在四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E.求证:AE=