如图,三角形abc中,AD是∠BAC的平分线,E,F分别是AB,AC上的点,且∠AED+∠AFD=180° 求证DE=D
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/15 19:04:12
如图,三角形abc中,AD是∠BAC的平分线,E,F分别是AB,AC上的点,且∠AED+∠AFD=180° 求证DE=DF
(1)求证:DE=DF
(2)若把条件∠AED+∠AFD=180°换成“DE=DF”,问,∠AED+∠AFD=180°吗,请说明理由.
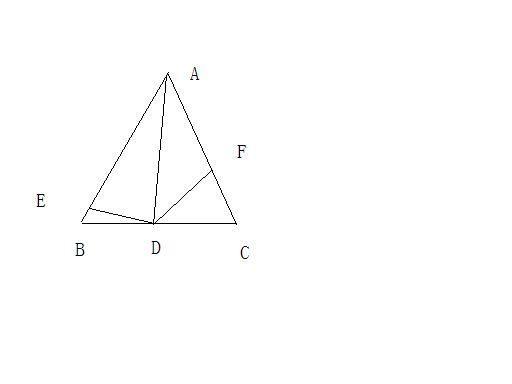
(1)求证:DE=DF
(2)若把条件∠AED+∠AFD=180°换成“DE=DF”,问,∠AED+∠AFD=180°吗,请说明理由.


1、证明:过点D作DM⊥AB于M,DN⊥AC于N
∵DM⊥AB,DN⊥AC
∴∠AMD=∠AND=90
∵AD平分∠BAC
∴DM=DN (角平分线性质)
∵∠AED+∠AFD=180, ∠AFD+∠CFD=180
∴∠AED=∠CFD
∴△DME≌△DNF
∴DE=DF
2、成立
证明:过点D作DM⊥AB于M,DN⊥AC于N
∵DM⊥AB,DN⊥AC
∴∠AMD=∠AND=90
∵AD平分∠BAC
∴DM=DN (角平分线性质)
∵DE=DF
∴△DME≌△DNF
∴∠AED=∠CFD
∵∠AFD+∠CFD=180
∴∠AED+∠AFD=180
∵DM⊥AB,DN⊥AC
∴∠AMD=∠AND=90
∵AD平分∠BAC
∴DM=DN (角平分线性质)
∵∠AED+∠AFD=180, ∠AFD+∠CFD=180
∴∠AED=∠CFD
∴△DME≌△DNF
∴DE=DF
2、成立
证明:过点D作DM⊥AB于M,DN⊥AC于N
∵DM⊥AB,DN⊥AC
∴∠AMD=∠AND=90
∵AD平分∠BAC
∴DM=DN (角平分线性质)
∵DE=DF
∴△DME≌△DNF
∴∠AED=∠CFD
∵∠AFD+∠CFD=180
∴∠AED+∠AFD=180
如图,三角形abc中,AD是∠BAC的平分线,E,F分别是AB,AC上的点,且∠AED+∠AFD=180° 求证DE=D
如图,在△ABC中,AD是∠BAC的平分线,E、F分别是AB、AC上的点,且DE=DF,问:∠AED+∠AFD=180°
如图,在△ABC中,AD是∠BAC的角平分线,E、F分别是AB、AC上的点,且∠AED+∠AFD=180°.(1)求证:
如图,在三角形ABC中,AD平分∠BAC,点E,F分别是AB,AC上的点,且∠AED+∠AFD求证DE=DF
已知在△abc中,ad是∠bac的平分线,e,f分别是ab,ac上的点.且∠aed+∠afd=180°
如图,在△ABC中,AD是∠BAC的角平分线,E、F分别是AB、AC上的点,且∠AED+∠AFD=180°.
如图,△ABC中,AD是角平分线,E、F分别为AC、AB上的点,且∠AED+∠AFD=180°.试问:DE与DF有何关系
如图所示,在三角形abc中,ad平分∠bac交bc于d,e,f分别是ab,ac上的点,若角aed+∠afd=180°,则
如图在△ABC中,AD是角BAC的平分线,E、F分别为AB、AC上的点且∠EDF+∠BAF=180°.(1)求证:DE=
如图,在△ABC中,AD是∠BAC的平分线,E、F分别是AB、AC上的点,且∠EDF+∠BAF=180°,求证:DF=D
在三角形ABC中,AD是角BAC的角平分线,E、F分别是AB、AC上的一点,且:∠BAC+∠EDF=180°,求证:DE
如图,△ABC中AD是角平分线,E,F分别为AC,AB上的点,且角AED+角AFD=180度.问DE与DF有何关系,为什