设f(x)=(x+1)ln(x+1)+m(x2+2x) (m∈R)

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/13 00:05:50

设f(x)=(x+1)ln(x+1)+m(x2+2x) (m∈R)
（1）当m=-1时,求函数f(x)的单调区间
（2）若当x≥0时,f(x)≤0,求实数m的取值范围

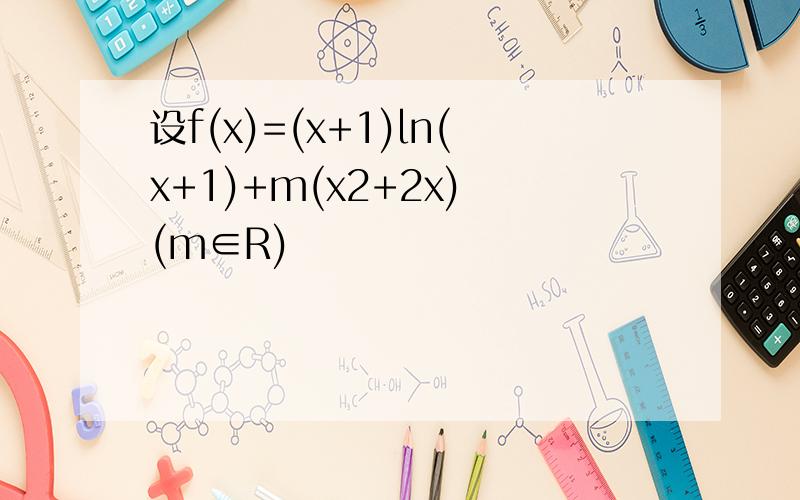
(1)定义域x+1>0,即x>-1.
f(x)=(x+1)ln(x+1)-x2-2x
f'(x)=ln(x+1)+1-2x-2=ln(x+1)-2x-1
令二阶导函数 f''(x)=1/(x+1)-2-1或x-1.令f''(x)>0解出来并综合定义域可知无解.所以一阶导函数f'(x)为定义域内的减函数.
所以f'(x)的最小值为x取无穷大时的极限值：负无穷大,最大值为x取-1时的极限值：负无穷小.所以f'(x)为一个能取到一切实数的减函数.所以总有一个x值使得f'(x)=0,但是我们无法求出来,它是个高等等式.暂且设这个值为x0.那么当f'(x)x0；当f'(x)>0时自然是x0.即g(x)为增函数,所以g(x)的最小值为当x=0时的极限值：1/2.
所以m
再问：洛米达法则是什么？
再答：对于两个多项式组成的商的形式，如果当变量趋向于某一个值时，分子上的多项式和分母上的多项式同时趋向于0或同时趋向于无穷大，这种情况下没有办法得到极限值了，就可以利用锣密达法则，即：对分子分母同时分别求导，此时的结果如果还是同时趋向于0或同时趋向于无穷大，就继续对分子分母同时求导，直到可以取到极限值为止。如果不懂锣密达法则，那这道题超出你的范围了！

设函数f（x）=x2+（m-1）x-2m-1（m∈R）, 设函数f(x)=x^2+ln(x+m). 设函数f(x)=x^2+m*ln(x+1) 绝对值不等式.设f（x）=ln（丨x-1丨+m丨x-2丨-3）（m属于R）（1）m=0时,f（x）的定义域（2）当0≤x 已知m∈R,设函数f（x）=x3-3（m+1）x2+12mx+1．设函数f（x）=x2+|x-2|-1，x∈R．已知f′（x）是f（x）的导函数，f（x）=ln（x+1）+m-2f′（1），m∈R，且函数f（x）的图象过点（0，-2 已知函数f(x)=(2x-a)/(x2+2) ,设方程f(x)=1/x的两根分别为x1,x2,是否存在m∈R,使m2+t 设函数f(x)=-1/3x^3+x^2+(m^2-1)x (x∈R),其中m>0 设函数f(x)=13x3+12(m-1)x2+x+2 设函数f（x）=-13x3+x2+（m2-1）x（x∈R），其中m＞0．设f（x）为定义在R上的奇函数，当x≥0时，f（x）=x2+2x+m（m为常数），则f（-1）=______．