有两个函数f(x)=asin(kx+π/3),g(x)=btan(kx-π/3)(k>0),已知它们的周期和为3π/2,
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/11 15:09:24
有两个函数f(x)=asin(kx+π/3),g(x)=btan(kx-π/3)(k>0),已知它们的周期和为3π/2,
且f(π/2)=g(π/2),f(π/4)=-√3g(π/4)+1,求a、b、k的值
且f(π/2)=g(π/2),f(π/4)=-√3g(π/4)+1,求a、b、k的值
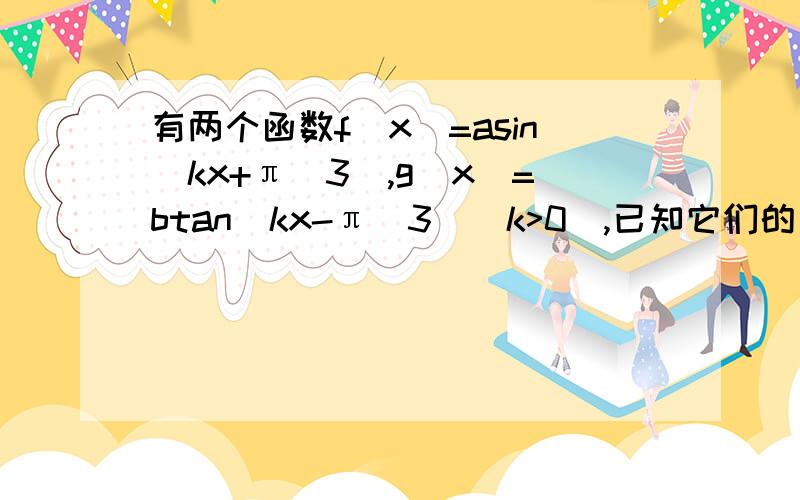
f(x)=asin(kx+π/3),g(x)=btan(kx-π/3)(k>0),
已知它们的周期和为2π/k+π/k=3π/2,
∴k=2.
又f(π/2)=g(π/2),f(π/4)=-√3g(π/4)+1,
∴-a(√3)/2=-b√3,a/2=-√3*b(1-√3)/(1+√3)+1,
化简得a=2b,b=b(2√3-3)+1,
解得b=(2+√3)/2,a=2+√3.
已知它们的周期和为2π/k+π/k=3π/2,
∴k=2.
又f(π/2)=g(π/2),f(π/4)=-√3g(π/4)+1,
∴-a(√3)/2=-b√3,a/2=-√3*b(1-√3)/(1+√3)+1,
化简得a=2b,b=b(2√3-3)+1,
解得b=(2+√3)/2,a=2+√3.
已知函数f(x)=asin(kx+π/3)和φ(x)=btan(kx-π/3),k>0
有两个函数f1(x)=asin(wx+π/3),f2(x)=btan(wx-π/3),w>0,已知他们的周期之和为3/
已知两个函数f(x)=asin(wx+π/3),g(x)=tan(wx-π/3),其中w大于0,它们的周期之和为3π/2
已知函数f(x)=2cos(kx+π/3)+b(k>0)的最小正周期为π,最小值为3
f(x)是以2为周期的偶函数, x∈[0,1]时,f(x)=x,若在区间[-1,3]内函数g(x)=f(x)-kx-k有
已知函数f(x)=2sin(x-π/3)+1,若函数y=f(kx)(k>0)的周期为2π/3,当x∈[0,π/3]时,方
设函数f(x)=sin(kx)+cos(kx)(k>0)的最小正周期为π,则k为 A.1 B.2
已知函数f(x)=3sin(kx/5+π/3)(k>0,k∈Z)
已知函数f(x)=(2x-3)/(kx^2+4kx+5)的定义域为R,求k范围.
已知函数f(x)=2sin(kx/5+π/3)(k≠0)
函数f(x)=2sin(x-π/3)+1,若函数y=f(kx)(k>0)的周期为2π/3,当x∈[0,π/3]时,方程f
已知函数f(x)=2sin(kx/5+pi/3)(k不等于0),求函数最大值和最小值和最小正周期;求最小正整数k,