∫Sinx^5 cosxdx-搜答案-神马作文网

∫sinx/(sinx-cosx)dx

∫sinx/(1+sinx)dx

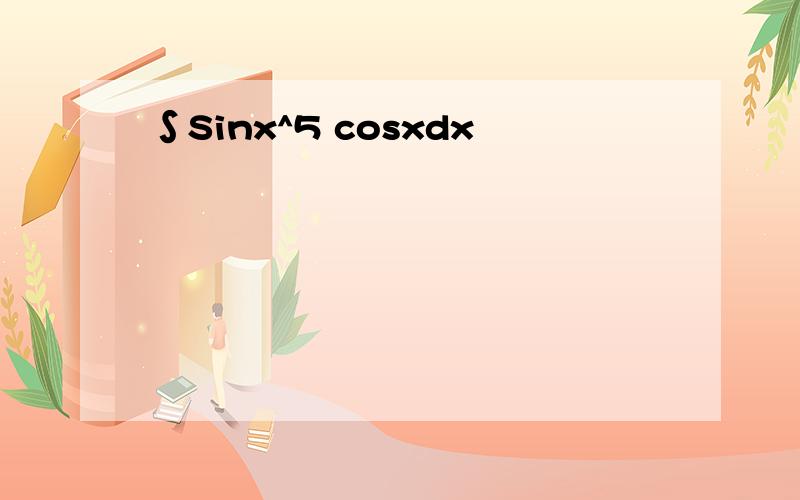
再问：但是这个的答案是2√3/3arctan(2tanx/2+1)/√3+c再问：呃，错了，答案是x-2/(1+tanx/2)再答：把我这个变形和你答案一样再问：哦哦，谢谢

充分应用公式：∫udv=u*v-∫vdu;∫du=∫u'dx1.：∫x^2(sinx)^2dx=∫x^2*(1-cos2x)/2dx=∫x^2/2dx-1/4*∫x^2*cos2xd(2x)对于∫x^

∫f(sinx)cosxdx=∫f(sinx)dsinx因为∫f(x)dx=1/(1+x^2)+c所以∫f(sinx)dsinx=1/[1+（sinx）^2]+c那么∫f(sinx)cosxdx=1/

∫【0到π/2】(sinx^10-cosx^10)dx/(5-sinx-cosx)=∫【0到π/2】sinx^10dx/(5-sinx-cosx)-∫【0到π/2】cosx^10dx/(5-sinx-

原式=∫(-2→0)(3x-1)dx+∫(0→2)(2x-1)dx+1/2∫(0→π/2)sin2xd2x=(3/2x²-x)|(-2→0)+(x²-x)|(0→2)-1/2cos

即∫f(x)=sinx/x+C∫f(sinx+1)cosxdx=∫f(sinx+1)d(sinx+1)=sin(sinx+1)/(sinx+1)+C

∫sin2/3xdx=3/2∫sin2x/3d2x/3=-3/2×cos(2x/3)+C∫e^sinxcosxdx=∫e^sinxdsinx=e^sinx+C∫1\x^2sin1\xdx=-∫sin(

解释：1、d代表的是微分(differentiation),dx代表的是x的无限小的增量；2、导数是dy/dx,我们教师近百年来,已经养成了一个全国性的通病：不喜欢写dy/dx,只喜欢写y',由于书写

我来做也

(f（cosx)sinx)'=-f(cosx)*sin^2(x)+f(cosx)cosx所以I=f（cosπ)sinπ-f（cos0)sin0=0

求∫ sinx/(1+sinx) dx

∫sinx/(1+sinx)dx=∫(sinx+1-1)/(1+sinx)dx=∫1dx-∫1/(1+sinx)dx后一个积分的分子分母同除以cosx=x-∫secx/(secx+tanx)dx=x-

∫(x²+5)cosxdx=∫x²cosxdx+5∫cosxdx=∫x²d(sinx)+5sinx=x²sinx-∫2xsinxdx+5sinx=x²

方法1：因为y=xcosx是奇函数,所以结果为零.这是高等数学中定积分的一个性质.方法2：如下图这个题目求原函数的方法超出了新课标的要求

∫[2,5](x^2)cosxdx=∫[2,5](x^2)dsinx=x^2sinx|[2,5]-∫[2,5]sinxd(x^2)=[25sin5-4sin2]-2∫[2,5]xsinxdx=[25s

∫sinx/(1-sinx)dx

参考以下∫sinx/(1+sinx)dx=∫(1+sinx-1)/(1+sinx)dx=∫[1-1/(1+sinx)]dx=∫dx-∫dx/(1+sinx)=x-∫dx/[sin²(x/2)

不好意思我学的不好看不懂题

∫x(sinx)∧5 dx

分部积分两次,之后解方程：再问：答案错了~~~~我知道怎么做了，谢谢~~~再答：应该是：A=(1/5)(e^π-2)。不好意思。