r2-x2-y2
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/20 23:02:46
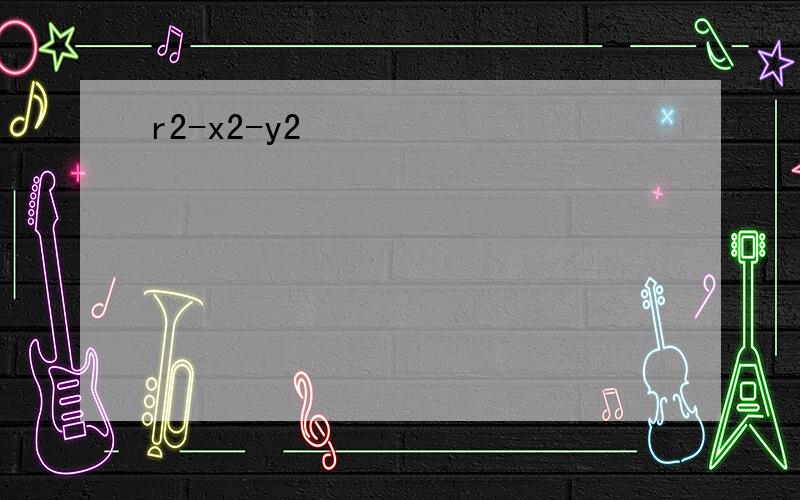
我就说外一条公切线吧,内公切线好像跟外的也差不多吧,首先能知道圆心距,用两点距离公式,然后连接两园圆心,画一条公切线,比如设与两圆分别交于A、B圆心分别为O1、O2.那么连接AO1,BO2设圆心连线与
点A,B在圆上,所以有xa^2+ya^2=r^2,xb^2+yb^2=r^2;PA垂直PB,所以应用向量的性质(xa-a)(xb-a)+(ya-b)(yb-b)=0;Q点坐标满足xq-xa=xb-a;
圆x2+y2=9的圆心(0,0),半径为3,圆x2+y2+8x-6y+25-r2=0(r>0)的圆心(-4,3),半径为:r,因为圆x2+y2=9与x2+y2+8x-6y+25-r2=0(r>0)相交
[(a+r)y-t(x+r)][(a-r)y-t(x-r)]+s(x^2+y^2-r^2)=0表示的是一条2次曲线,经过四点P,Q,A1,A2.其中s是一个参数,你想像s越大,这个曲线越像圆,s越小,
x2+y2-2x+2y=0(x-1)^2+(y+1)^2=2中心坐标(-1,1),R=√2中心坐标到原点距离=√2则0
答:圆x^2+y^2=r^2与圆x^2+y^2+6x-8y=0(x+3)^2+(y-4)^2=25半径R=5,圆心(-3,4),r>0两圆相交,则圆心距小于半径之和大于半径之差圆心距d=√[(-3-0
1.直线l:y=kx+1是恒过点(0,1)的直线系,只要点(0,1)在圆C:x2+y2=r2内部就恒有两个不同的交点.0+1<r2,r>0,则r>1.2.将y=kx+1代入x2+y2=r2设A(x1,
∵两圆外切,∴两圆圆心距等于两圆半径之和,∴9+1=2r,∴r=102,故选C.
球坐标变换,然后得到:原积分=∫(0到2∏)dΘ∫(0到П)sinφdφ∫(0到1)r^4dr=2П*2*(1/5)=4П/5.
错了,应该是P在圆内则√(x0²+y0²)1/r圆心到直线距离是|0+0-r²|/√(x0²+y0²)=r²/√(x0²+y0&s
(1)由圆C:x2+y2=r2,再由点(1,3)在圆C上,得r2=12+(3)2=4所以圆C的方程为x2+y2=4;(2)假设直线l存在,设A(x1,y1),B(x2,y2),M(x0,y0)①若直线
(1)∵圆O:x2+y2=r2(r>0)与直线x-y+22=0相切,∴圆心O到直线的距离d=2212+(−1)2=2=r,∴圆O的方程为x2+y2=4; (2)若直线
OP的斜率是K=yo/xo那么切线的斜率是k'=-1/k=-xo/yo故切线的方程是y-yo=-xo/yo*(x-xo)即有yoy-yo^2=-xox+xo^2即有xox+yoy=xo^2+yo^2=
9中可能有:(a)⇒(1),(a)⇒(2),(a)⇒(3),(b)⇒(1),(b)⇒(2),(b)⇒(3),(c)⇒(1),(c)⇒(2),(c)⇒(3).所以可能是真命题的是:(a)⇒(2),(b)
由题意知,OA⊥PA,BO⊥PB,∴四边形AOBP有一组对角都等于90°,∴四边形AOBP的四个顶点在同一个圆上,此圆的直径是OP,圆x2+y2=r2(r<5)的圆心(0,0),OP=5,∴四边形AO
圆心为(a,b),过圆上M(x0,y0)的切线方程是(x-x0)(x0-a)+(y-y0)(y0-b)=r^2[r^2=(x0-a)^2+(y0-b)^2]利用向量垂直做比较简单
这个式子是可以推到出来的,式子以后记住就可以直接用了,很方便.利用点斜式求切线.有点了,差一斜率,圆心与已知点的连线与切线垂直,其斜率=b/a,又根据两条直线互相垂直,则斜率相乘得-1.所以切线的斜率
x2+y2=4表示的是以(0,0)为圆心,半径是2的圆(只有那条闭合的曲线)那么这里加上一个小于,就是说,这表示(0,0)为圆心、半径是2的圆面,是一个面,而不是上面的一条线.
设B(2+r,yB),C(2+r,-yB)AB直线方程:k(x+4)-y=0,G点(2,0)到AB的距离为r,|k(2+4)|=r*√(k^2+1),得k^2=r^2/(36-r^2).1k=yB/(