limtanπx 2*ln(2-x)
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/11 22:08:55
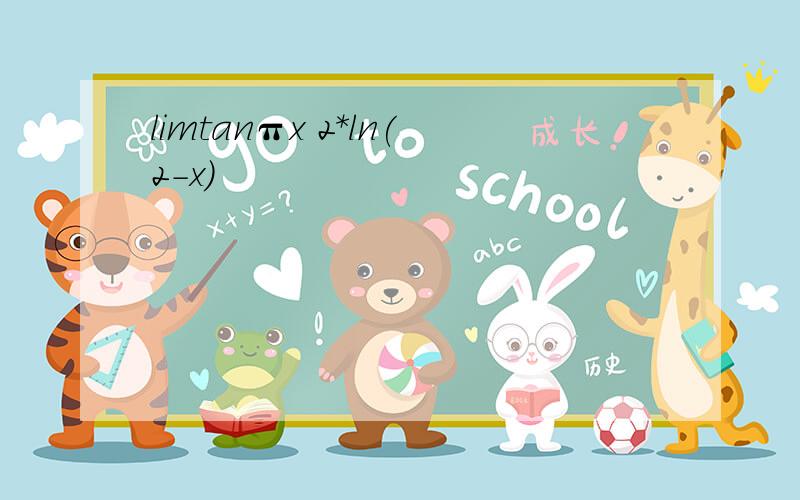
已知函数f(x)=ln(x-2)-x2/2a,求函数f(x)的单调区间解析:∵函数f(x)=ln(x-2)-x2/2a,其定义域为x>2令f’(x)=1/(x-2)-ax=0==>ax^2-2ax-1
f(x)=a/(1+ax)+2x-a
因为函数f(x)=ln(x2+x+1-x2-x+1)=ln((x+12)2+(0-32)2-(x-12)2+(0-32)2),真数的值可看作在x轴上一点P(x,0)到点(-12,32)与点(12,32
分步积分∫ln(1+x^2)dx=x*ln(1+x^2)-∫2x^2/(1+x^2)dx对后面的进行分离=x*ln(1+x^2)-∫2dx+∫2/(1+x^2)dx直接积分=x*ln(1+x^2)-2
f(x)=ln(x+1)-x+x^2/2f'=1/(x+1)-1+x=(x^2+x-x-1+1)/(x+1)=(x^2)/(x+1)当x>0时,f'=(x^2)/(x+1)>0f(x)=ln(x+1)
f(x)=ln√(x2+1),f'(x)=1/√(x²+1)*(1/2)/√(x²+1)*2x=x/(x²+1)f'(2)=2/(4+1)=2/5
f'(x)=(2x-1)/(x²-x-2)再问:那单调递增区间呢?再答:x²-x-2=(x-2)(x+1)=(x-1/2)²-9/4定义域为x>2,或x2
f(x)的定义域为(-32,+∞)(1)f′(x)=22x+3+2x=4x2+6x+22x+3当-32<x<-1时,f′(x)>0;当-1<x<-12时,f′(x)<0;当x>-12时,f′(x)>0
原式配个+1-1得到In{arctanx/x+1-1}/x2用等价无穷小arctanx-1/x3再洛必达(1/1+x2)-1/x3最后变成-1/3+3x2得到-1/3
(Ⅰ)由题意,得4−2a+2>04+2a+2≤0,(2分)所以a≤-3.故实数a的范围为(-∞,-3].(4分)(Ⅱ)由题意,得x2+ax+2>0在R上恒成立,则△=a2-8<0,(6分)解得-22<
令g(x)=-x^2-2x+8=-(x^2+2x-8)=-(x+4)(x-2)=-(x+1)^2+9定义域为g(x)>0,得-4
y'=[(4x^3+2x)(x^2+2)/(x^4+x^2)-2xln(x^4+x^2)]/[x^2+2]^2=[(4x^3+2x)(x^2+2)-2x^3(x^2+1)ln(x^4+x^2)]/[(
1.f’(x)=2x+a/(1+x)=0,2x^2+2x+a=0有不等的实根,4-8a>0,a
f(x)=x-1/x+2+ln(x2+1)f'(x)=1+1/x^2+2x/(x^2+1)
要使函数f(x)=1/ln(x*2)*√4*x2有意义必须有:ln(x*2)≠0x²≠0,2x>0,2x≠1解得,函数f(x)=1/ln(x*2)*√4*x2;的定义域为:x>0且x≠1/2
因为ln(1+x-2x2)=ln(1-x)+ln(1+2x),故只需计算ln(1-x)以及ln(1+2x)的幂级数展开式即可.在−1≤x<1中,ln(1−x)=∞n=1(−1)n−1(−x)nn=∞n
你好!本题需要用到泰勒公式详解如图
由x2-2x>0,可得x<0或x>2∵t=x2-2x=(x-1)2-1的单调增区间是(1,+∞),y=lnt在(0,+∞)上单调增∴函数y=ln(x2-2x)的单调增区间是(2,+∞),故选D.