四面体A-BCD中,∠ABC=∠ABD=

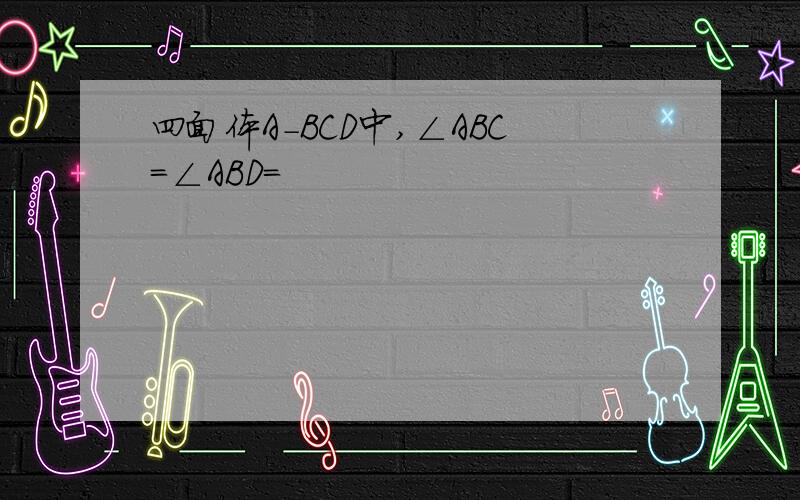
=AC=1,BAC=90度BC=根号2设A点坐标为(0,0),B为(0,1),C为(1,0)角ACD=4560=105度D坐标为(1根号2*cos75度,根号2*sin75度)直线AD的斜率为根号2*

题目是不是打错了?平面BCD⊥平面BCD?

过点B作CD的垂线,垂足为M则平面ABM与线段CD垂直过点C作BD的垂线,垂足为N则平面ACN与线段BD垂直设BM和CN的交点为O,连接DO,并延长到BC,交BC于点P则DP⊥BC∵平面ABM和平面A

做出来了,构造一个三棱柱∠BAD=30°或150°AB=a,CD=b三棱柱的高为d四面体B-CDB’,D-ABD'的体积是三棱柱的1/3所以四面体A-BCD的体积也是三棱柱的1/3而底面积=1

5775827743272567832

向量法：AC^2=(AB+BC)^2=(AD+DC)^2则有：AB^2+2AB·BC+BC^2=AD^2+2AD·DC+DC^2根据AB=AD,CB=CD整理两式得：AB·BC=AD·DC；AC·BD

证明：在Rt△ABC中，∠A+∠B=90°（直角三角形两锐角互余），∵CD⊥AB，∴∠CDB=90°，∴∠BCD+∠B=90°（直角三角形两锐角互余），∴∠A=∠BCD（同角的余角相等）．

解,过点A作AE⊥平面BCD,由该四面体的性质可知,该点在DG的延长线上；AG=√3/2BC;BC=√2BD=2所以AG=√3/2*√2=√6/2在三角形AGD中,cosAGD=-√3/3；∠AGD+

连OA、OB、OC、OD则VA-BEFD＝VO-ABD＋VO-ABE＋VO-BEFD,VA-EFC＝VO-ADC＋VO-AEC＋VO-EFC又VA-BEFD＝VA-EFC而每个三棱锥的高都是原四面体的

延长BO，交CD于点N，可得BN⊥CD且N为CD中点设正四面体ABCD棱长为1，得等边△ABC中，BN=32，∵AO⊥平面BCD，∴O为等边△BCD的中心，得BO=33，Rt△ABO中，AO=63，设

作AH⊥平面BCD,垂足H,连结并延长BH交CD于E,在平面ABE中作EF⊥AB,垂足F,AB⊥CD,（已知）,根据三垂线逆定理,CD⊥BE,CD⊥平面ABE,四面体A-BCD体积分成二部分,即C-A

设E为BD中点,连接AE,CE.下面证明AE垂直于面BCD：由AB=AD=1,E为BD中点,则AE垂直于BD在RT△BCD中,BD=(BC^2+CD^2)^O.5=根号3,E为BD中点,则CE=BE=

﹙√6/3﹚aarccos√3/3

取BD中点M,连AM,CM,则∠AMC为二面角A-BD-C的平面角,容易算得：AM=CM=√2a/2,在△AMC中,AM=CM=√2a/2,AC=aAM²+CM²=AC²

证明：连结AE,DE因为AB=AC,BD=CD,点E是棱BC的中点所以AE⊥BC,DE⊥BC又AE和DE是平面ADE内的两条相交直线则由线面垂直的判定定理可得：BC⊥平面ADE因为AD在平面ADE内所

∵四面体A-BCD中，共顶点A的三条棱两两互相垂直，且AB=AC=1，AD＝2故四面体的外接球即为以AB，AC，AD为长宽高的长方体的外接球可求得此长方体的体对角线长为2则球半径R=1弦BD=3则co

相当于两个这样四面体底面重合成长方体外接于球,长对角线是外接圆的直径,半径=(a^2+b^2+c^2)/2.或者,三角形SAB中从S作边AB中线延长一倍到点D,CD是外接圆直径

将四面体P-ABC的侧面沿PA剪下再展开，得到如图所示五边形（左图）∵四面体P-ABC中，PA=PB=PC=2，∠APB=∠BPC=∠APC=30°∴展开图中∠A'PA=3×30°=90°连接AA'，

四面体A-BCD中EFGH分别为ABBCCDDA中点（1）若AC=BD求证EFGH为菱形由四面体A-BCD中EFGH分别为ABBCCDDA中点,得EH//BD//FG,且EH=0.5BD=FGEF//

∵AB=AC∴∠b=∠acb.∵∠a=180°-2∠b∠b+∠bcd=90°所以∠b=90°-∠bcd∴∠a=180°-2（90°-2∠bcd）=180-180+2∠bcd∴∠a=2∠bcd