如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上．求证：BC=AB+DC．

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/19 07:51:32

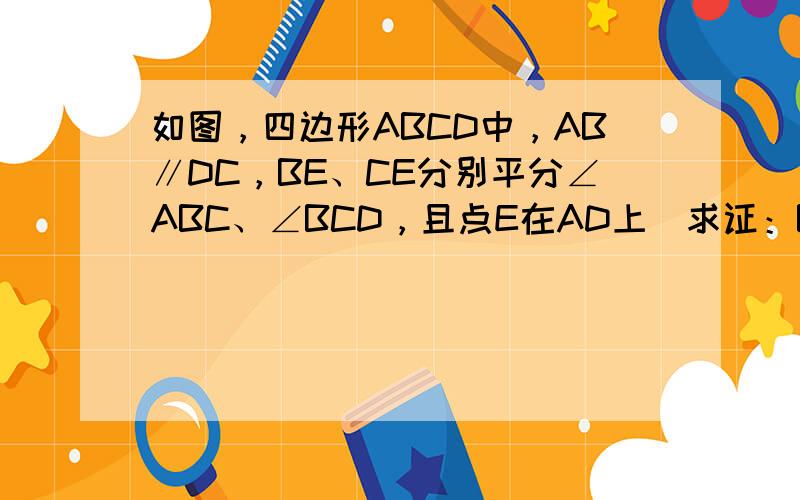
证明：延长BE交CD的延长线于点F，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∵AB∥CD，
∴∠F=∠ABE，∠A=∠FDA，
∴∠F=∠CBE，
∴CF=BC，
∵CE平分∠BCD，
∴BE=EF（三线合一）），
在△ABE和△DFE中，

∠F＝∠ABE
EB＝EF
∠AEB＝∠DEF，
∴△ABE≌△FDE（ASA），
∴FD=AB，
∵CF=DF+CD，
∴CF=AB+CD，
∴BC=AB+CD．

如图,四边形ABCD中,ab平行dc,be、ce分别平分∠abc、∠bcd,且点e在ad上.求证：BC=AB+DC 如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上．求证：BC=AB+DC．如图,四边形ABcD中,AB平行于Dc,BE、cE分别平分角ABc、角BcD,且点E在AD上,求证：Bc=AB+Dc 如图,在四边形abcd中,点p在ad上,pb平分∠abc,pc平分∠bcd,且ab∥dc,求证ab+cd=bc 如图，在四边形ABCD中，AD∥BC，AE平分∠BAD交DC于点E，连接BE，且AE⊥BE，求证：AB=AD+BC．如图在四边形ABCD中AB╱╱CD,BE CE分别平分∠ABC与∠DCB,E在AD上.求证BC=AB+CD 已知：如图，在梯形ABCD中，AD∥BC，AB=DC，点E、F分别在AB、DC上，且BE=2EA，CF=2FD．求证：∠ 如图,在等腰梯形ABCD中,AB平行DC,AB=DC,E,F,G,H分别为AD,BE,BC.CE的中点.求证：四边形EF 如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD⊥DC，BD=DC，CE平分∠BCD，交AB于点E，交BD 已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E．求证：如图，梯形ABCD中，AD∥BC，E为AB中点，且AD+BC=DC，求证：DE⊥EC，DE平分∠ADC，CE平分∠BCD 在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BE=DC,CE平分∠BCD,交AB于点E,下列结论：