设函数f(x)=x2+ax+b,且方程f(x)=0在区间(0,1)和(1,2)上各有一解,则2a-b的取值范围用区间表示
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/19 08:57:27
设函数f(x)=x2+ax+b,且方程f(x)=0在区间(0,1)和(1,2)上各有一解,则2a-b的取值范围用区间表示为______.
 ∵函数f(x)=x2+ax+b,且方程f(x)=0在区间(0,1)和(1,2)上各有一解,
∵函数f(x)=x2+ax+b,且方程f(x)=0在区间(0,1)和(1,2)上各有一解,则函数f(x)=x2+ax+b在区间(0,1)和(1,2)上各有一个零点,
又∵f(x)=x2+ax+b是开口向上的抛物线,∴f(1)<0,f(2)>0,f(0)>0.
∴f(1)=a+b+1<0…①,
f(2)=4+2a+b>0…②,
f(0)=b>0…③
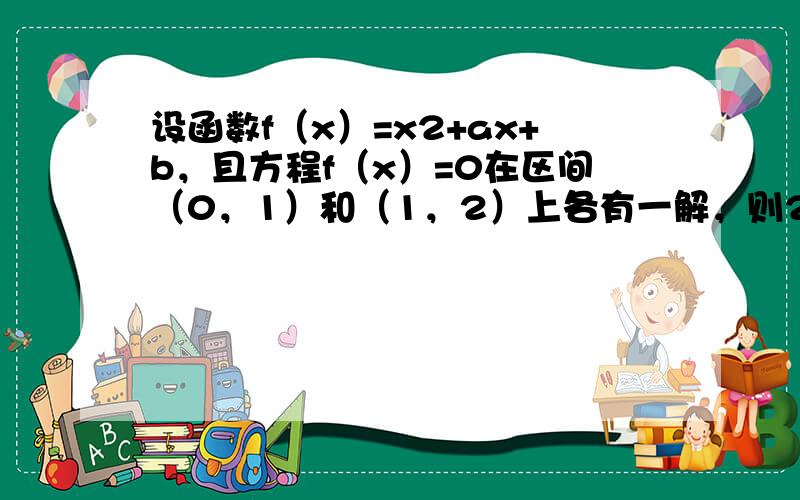
画出约束条件①②③表示的可行域如图:则2a-b=z,
经过可行域的A点即
a+b+1=0
4+2a+b=0,解得A(-2,3)时取得最小值为:-8,
经过B
a+b+1=0
b=0即B(-1,0),2a-b取得最大值-2,
2a-b的取值范围用区间表示为(-8,-2)
故答案为:(-8,-2).
设函数f(x)=x2+ax+b,且方程f(x)=0在区间(0,1)和(1,2)上各有一解,则2a-b的取值范围用区间表示
函数f(x)=x^2-ax+2b的零点一个在区间(0,1)上,另一个在区间(1,2)上,则2a+3b的取值范围是?
函数f(x)=2x2+ax+b在区间(-∞,4]上为减函数,求实数a的取值范围.
设定义在区间(-b,b)上的函数f(x)=lg1+ax /1-2x 是奇函数(a,b∈R,且a≠-2),则a^b的取值
设a,b∈R,且a≠2,定义在区间(-b,b)内的函数f(x)=lg(1+ax/1+2x)是奇函数.①求b的取值范围 ②
设函数f(x)=x2+(b+2)x+c(b,c∈R)在区间(0,1)上不单调,则b的取值范围是______.
设函数f(x)=x的三方+ax-2在区间[1,+∞)上是增函数,则实数a的取值范围?
设函数f(x) =x ^3十ax一2在区间(1,正无穷)上是增函数,则实数a的取值范围
设函数f(x)=x^3+ax-2在区间(1,正无穷)上是增函数,则a的取值范围是_____________
已知函数f(x)=ax^2+bx-1(a,b属于R且a>0)有两个零点,其中一个零点在区间(1,2)内,则的取值范围为?
设a,b属于R,且a不等于2定义在区间(-b,b)上的函数f(x)=lg(1+ax)/(1+2x)为奇函数则b取值范围
设函数f(x)=(ax+1)/(x+2a)在区间(-2,+无穷)上是增函数,那么a的取值范围是?