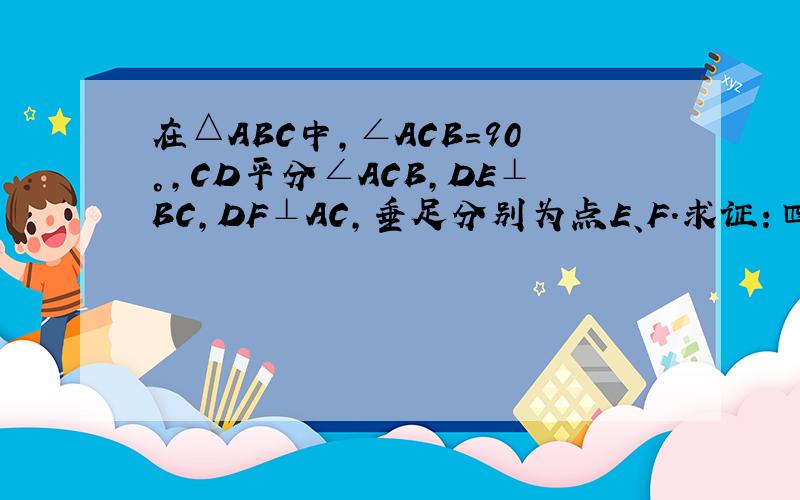
在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为点E、F.求证:四边形CEDF是正方
在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为点E、F.求证:四边形CEDF是正方
如图△ABC中,∠ACB=90°,CD平分∠ACB交AB于D,DE⊥BC于E,DF⊥AC于F,求证:四边形CEDF是正方
已知,如图△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F.求证:四边形CFDE
如图,在△ABC中∠ACB=90°,点D在AB上,且CD平分∠ACB,过点D作DE⊥AC,DF⊥BC,垂足分别为点E、F
△ABC中,CD是∠ACB的平分线,DE⊥BC,DF⊥AC,垂足分别为E.F.要使四边形CEDF是正方形,需要添加什么条
如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E,F.若CE=2,求四边形CE
在直角三角形ABC中,∠ACB=90°,CD平分∠ACB,过D点分别作DE⊥BC,DF⊥AC,垂足分别为E、F.
如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC,DF垂直BC,DF⊥AC,垂足分别为E、F.若CE=2
已知Rt△ABC中,∠ACB=90°,CD平分∠ACB,且DE⊥AC,DF⊥BC.求证:四边形DECF是正方形.
如图在RT三角形ABC中∠ABC=90°CD平分∠ACB 过点D分别作DE⊥BC DF⊥AC 垂足分别为E F
平行四边形,证明题如图,三角形ABC中,角ACB=90°,CD平分角ACB,DE⊥BC,DF⊥AC,垂足分别为E、F,试
如图,三角形ABC中,角ACB=90°,CD平分角ACB,DE垂直BC,DF垂直AC,垂足分别为E,F.求证四边形CFD