如图所示，矩形纸片ABCD中，AB=4cm，BC=3cm，把∠B、∠D分别沿CE、AG翻折，点B、D分别落在对角线AC的

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/11 09:13:07

如图所示，矩形纸片ABCD中，AB=4cm，BC=3cm，把∠B、∠D分别沿CE、AG翻折，点B、D分别落在对角线AC的点B′和D′上，则线段EG的长度是

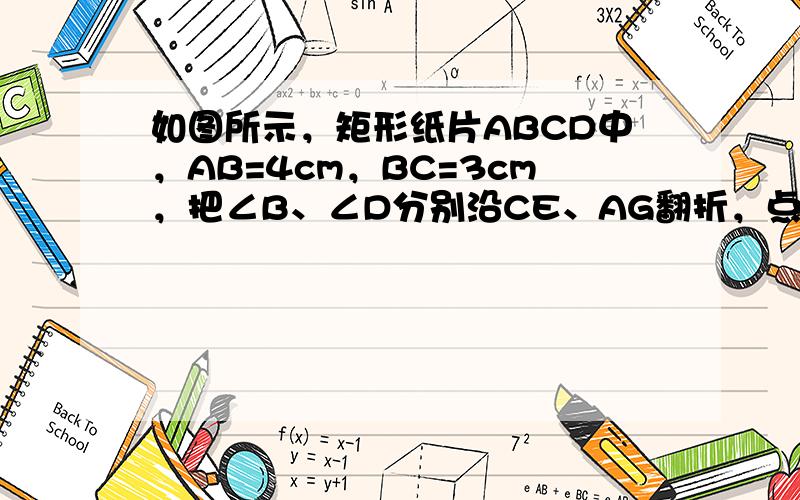
连接GE交AC于点O，
由题意，得∠GAD′=
1
2∠DAC，∠ECB′=
1
2∠BCA，
∵四边形ABCD为矩形，
∴AD∥BC，
∴∠DAC=∠BCA，
∴∠GAC=∠ECA，
∴AG∥CE，
又∵AE∥CG
∴四边形AECG是平行四边形，
∴OG=OE，
∵矩形纸片ABCD中，AB=4cm，BC=3cm，
∴△ABC是直角三角形，
∴AC=
AB2+BC2=
42+32=5cm，
∵△AGD′由△AGD翻折而成，
∴∠GD′A=∠D=90°，AD′=AD=3cm，
同理可得，CB′=3cm，
∴B′D′=1cm，
∴OD′=
1
2cm，
设DG=x，则GD′=x，GC=4-x，CD′=AC-AD′=5-3=2，
∵在Rt△GCD′中，GC²=GD′²+CD′²，即（4-x）²=x²+2²，解得x=1.5，
∴GD′=
3
2cm，
∵在Rt△GOD′中，GD′=
3
2，OD′=
1
2，GO²=GD′²+OD′²，
∴GO=
(
3
2)2+(
1
2)2=

10
2cm，
∴EG=2GO=2×

如图所示，矩形纸片ABCD中，AB=4cm，BC=3cm，把∠B、∠D分别沿CE、AG翻折，点B、D分别落在对角线AC的如图,ABCD是矩形纸片,翻折∠B,∠D,使BC,AD恰好落在AC上．点B,D分别落在F,H上,CE与AG是折痕如图，ABCD是矩形纸片，翻折∠B、∠D，使BC、AD恰好落在AC上．设F、H分别是B、D落在AC上的点，E、G分别是折矩形纸片ABCD中,AB=4cm,AD=3cm,把矩形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长为如图：ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC （2010•宝安区一模）如图所示，已知梯形纸片ABCD中，∠B=60°，将纸片沿着对角线AC折叠，折叠后点D刚好落在AB 如图,已知矩形纸片ABCD.AB=2√2cm,BC=1cm,若将纸片沿AC对折成如图所示的形状,点B落在点B′处,求线段在矩形ABCD中,AB=3,BC=4,将矩形ABCD沿CE折叠,使D′恰好落在对角线AC上的F处如图：ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是如图ABCD是矩形纸片，翻折∠B、∠D使BC边、AD边恰好落在AC上，设F、H分别是B、D落在AC上的两点，E、G分别是如图ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上．设F、H分别是B、如图,把一张矩形纸片沿对角线AC折叠,使点D落在点D~处,AD~交BE与E,AD=8cm,AB=4cm.求三角形ACE的