已知,把RT△ABC和RT△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB＝∠ED

来源：学生作业帮编辑：神马作文网作业帮分类：综合作业时间：2024/11/11 11:37:57

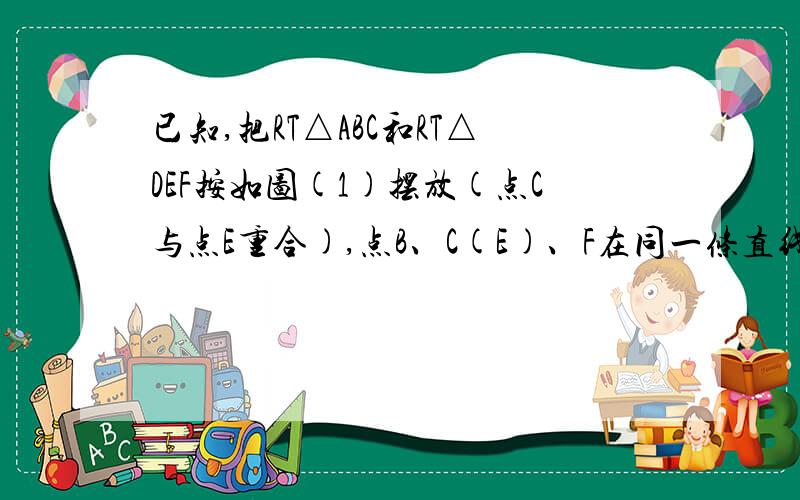
已知,把RT△ABC和RT△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB＝∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.

1）∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF＋∠ACB＋∠EQC = 180°,
∴∠EQC = 45°.
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知：CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8－t.
在Rt△ABC中,由勾股定理得：AB = 10 cm .
则AP = 10－2 t.
∴10－2 t = 8－t.
解得：t = 2.
答：当t = 2 s时,点A在线段PQ的垂直平分线上.········ 4分
（2）过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,
∴ .∴PM = .
∵BC = 6 cm,CE = t,∴ BE = 6－t.
∴y = S△ABC－S△BPE =－= －
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答：当t = 3s时,四边形APEC的面积最小,最小面积为cm2.··············· 8分
（3）假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
∴.
∵,∴△PAN ∽△BAC.
∵NQ = AQ－AN,
∴NQ = 8－t－() = ．
∵∠ACB = 90°,B、C（E）、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ .∴ .
∵ ∴
解得：t = 1.
答：当t = 1s,点P、Q、F三点在同一条直线上.

已知,把RT△ABC和RT△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB＝∠ED 已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合）,点B、C（E）、F在同一条直线上．∠ACB=∠ED 已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上. 已知直角三角形ABC和直角三角形DEF按图一摆放（C与E重合）,点B,C(E),F在同一条直线上,∠ACB=∠EDF=9 在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点（点D不与B、C重合）,直线BE⊥AD于点E,交直线AC于点F （2014•沙坪坝区二模）已知等边△ABC和Rt△DEF按如图所示的位置放置，点B，D重合，且点E、B（D）、C在同一条已知在下图中,将一副三角形(RT△ABC和△DEF)如图①摆放点E,A,D,B在一条直线上且D 如图,在RT△ABC中,∠ACB=90°,∠B=30°,BC=4,△DEF为等边三角形,点E、F在BC边上当点F与点C重如图,已知点B,F,C,E,在同一条直线上,bc=ef,ab∥de,ac∥df,△abc与△def是否全等? 已知：将一副三角板（Rt△ABC和Rt△DEF）如图①摆放，点E、A、D、B在一条直线上，且D是AB的中点．将Rt△DE 已知:将一副三角板(RT△ABC和RT△DEF)如图①摆放,点E,A,D,B在一条直线上,且D是AB的重点.将RT△DE 如图,已知点b,f,c,e在同一条直线上,bc等于ef,ab平行de,ac平行df,三角形abc与三角形def是否全等