如图,圆0中两条相等的弦AB,CD分别延长到E,F,使BE=DF（1）求证：EF的垂直平分线必过圆心.（2）若AB与CD

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/12 20:24:05

如图,圆0中两条相等的弦AB,CD分别延长到E,F,使BE=DF（1）求证：EF的垂直平分线必过圆心.（2）若AB与CD在圆0内相较于P,同样延长AB,CD,使BE=DF,那么是否还有（1）中的相同的结论,请说明理由（如图2）

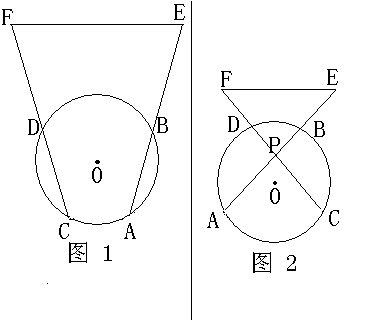
1.AB=CD
∠AOB=∠COD,又∠ODB=∠CBD
所以∠BDF=∠EDB,BE=DF
所以EF‖BD
EF垂直平分线也垂直平分BD
BD为圆O弦
所以EF垂直平分线必过圆心O
2.连接BD,作OV垂直DB,延长与EF交于点Q,作AB,CD的圆心距OI,OL
∵OV⊥DB
∴OV平分DB（即OV是DB的中垂线）
∵AB=CD
∴OI=OL
∵OD=OB=r,∠OIB=∠OLD
∴△OIB≌△OLD
∠PDO=∠PBO
∵OD=OB
∴∠ODB=∠OBD
∴∠ODB+∠PDO=∠OBD+∠PBO（即∠PDB=∠PBD)
∴DP=BP（△PDB是等腰三角形)
∵DF=BE
∴DP+DF=BP+BE（即PF=EF,△PFE是等腰三角形)
根据等腰三角形的三线合一可知△PDB中∠DPB的平分线即是DB的中垂线OV,同理得在等腰三角形PEF中∠DPB也是EF的中垂线OQ,所以OV与OQ在同一直线上,EF的垂直平分线必过圆心O

如图,圆0中两条相等的弦AB,CD分别延长到E,F,使BE=DF（1）求证：EF的垂直平分线必过圆心.（2）若AB与CD 如图,圆O中两条相等的弦AB,CD分别延长到E,F,使BE=DF求证EF的垂直平分线必过圆心在圆O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF,求证：EF的垂直平分线经过点O 已知：在⊙O中,弦AB=CD,延长AB到E,延长CD到F,使BE=DF.求证：EF的垂直平分线经过点O 如图,在平行四边形ABCD中,延长AB到E,延长CD到F,使得BE=DF,求证；AC与EF互相平分如图,在⊙O中,弦AB=CD,延长AB到点E,延长CD到点F,使得BE=DF,过点O作OP⊥EF,垂足为点P.求证：PE 如图,梯形ABCD中,AB平行CD,且AB=2CD,E,F分别是AB,CD的中点,EF与BD相交与点M,（1）求证△ED 如图,在平行四边形ABCD中,延长AB到E,使BE=1/2AB,延长CD到F,使DF=DG,EF交BC于G,交AD于H, 如图,在平行四边形ABCD中,延长AB到E,使BE=1/2AB,延长CD到F,使DF=DG,EF交BC于G,交AD于H 如图,已知∠BED=∠B+∠D,试说明AB与CD的位置关系.(提示:延长BE交CD于点F,或过E作EF∥AB均可）已知如图AB平行于CD AD交BC于点O EF过点O 分别交AB CD于点E F 且AE=DF 求证O是EF的中点(过如图,已知OP为线段AB的垂直平分线AC BE分别交圆O与C D和E F且CD=EF 求证AD=BF