三角形内角ABC的对边为a,b,c,已知2a=根号3c,cosC=根号3/4 1、求s
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/20 11:02:09
三角形内角ABC的对边为a,b,c,已知2a=根号3c,cosC=根号3/4 1、求s
三角形内角ABC的对边为a,b,c,已知2a=根号3c,cosC=根号3/4
1、求sinB的值
2、若D为AC中点,且三角形ABD的面积为根号39/8,求BD的长
三角形内角ABC的对边为a,b,c,已知2a=根号3c,cosC=根号3/4
1、求sinB的值
2、若D为AC中点,且三角形ABD的面积为根号39/8,求BD的长
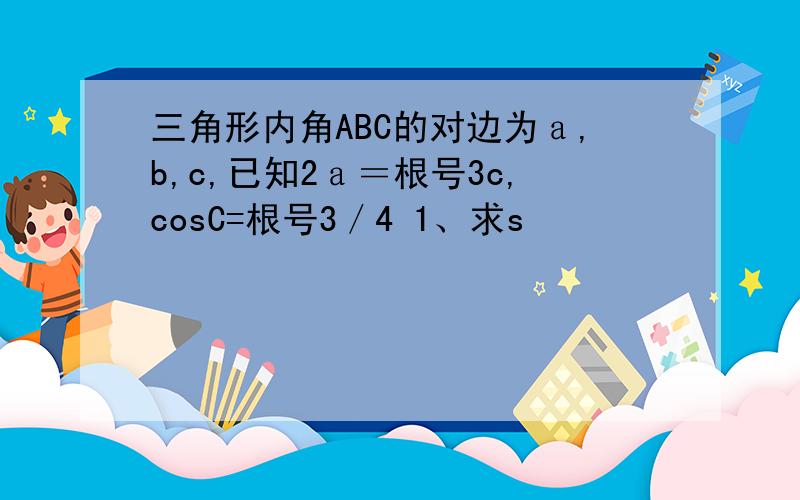
2a=√3 c,a=√3/2 c
c^2=a^2+b^2-2abcosC
3/4c^2+b^2-√3/2 * √3/2cb-c^2=0
b^2-3/4cb+c^2/4=0
(b-c)(b+c/4)=0
得b=c,另一个舍去
所以sinB=sinC=√(1-3/16)=√13/4
2、a/c=sinA/sinC=√3/2,得sinA=√39/8 (提示一下,sinC=sinB)
所以S△ABD=0.5*c*0.5bsinA=√39/8 ,则c=b=2
所以BD^2=c^2+(0.5b)^2-2*c*0.5b*cosA=4+1-4*5/8
BD=√10/2
c^2=a^2+b^2-2abcosC
3/4c^2+b^2-√3/2 * √3/2cb-c^2=0
b^2-3/4cb+c^2/4=0
(b-c)(b+c/4)=0
得b=c,另一个舍去
所以sinB=sinC=√(1-3/16)=√13/4
2、a/c=sinA/sinC=√3/2,得sinA=√39/8 (提示一下,sinC=sinB)
所以S△ABD=0.5*c*0.5bsinA=√39/8 ,则c=b=2
所以BD^2=c^2+(0.5b)^2-2*c*0.5b*cosA=4+1-4*5/8
BD=√10/2
三角形内角ABC的对边为a,b,c,已知2a=根号3c,cosC=根号3/4 1、求s
三角形ABC中为内角A,B,C的对边分别为a,b,c,已知2a=根号3c,cosc=4分之根号3,求sinB的值.
△ABC中内角A,B,C的对边分别为a,b,c,已知2a=根号3c,cosC=根号3/4
三角形ABC中内角A,B,C的对边分别为a,b,c,已知2a=根号3c,cosC=根号3/4.(I)求sinB的值.(I
在三角形abc中,内角a,b,c的对边分别为a,b,c,已知(根号3sinb-cosb)(根号3sinc-cosc)
三角形ABC的内角ABC的对边分别为abc,已知b=3,三个内角ABC成等差数列,cosC=根号6/3,求c
已知△ABC的三个内角A.B.C的对边分别为a.b.c,且△ABC的面积为S=2分之根号3×ab×cosC (1)若a=
在三角形ABC中,内角A,B,C的对边a,b,c,已知cosA=2/3,sinB=根号5cosC,(1)求tanC的值.
在三角形ABC中,内角A,B,C所对的边长分别为a,b,c.已知cosA=2/3,sinB=根号5cosC 1.求tan
在三角形ABC中,内角A,B,C的对边分别是a,b,c已知C=2,C=π/3(1)若三角形ABC的面积为根号3求a,b
已知a,b,c分别为三角形ABC三个内角A,B,C的对边acosC+根号3asinC-b-c=o.求A
已知三角形ABC的内角A、B、C的对边分别为a、b、c,根号3sinCcosC-cos方C=1/2,