已知：ABC是直角三角形,∠BCA=90,CM、BN分别为AB、AC边上的中线,

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/11 08:41:12

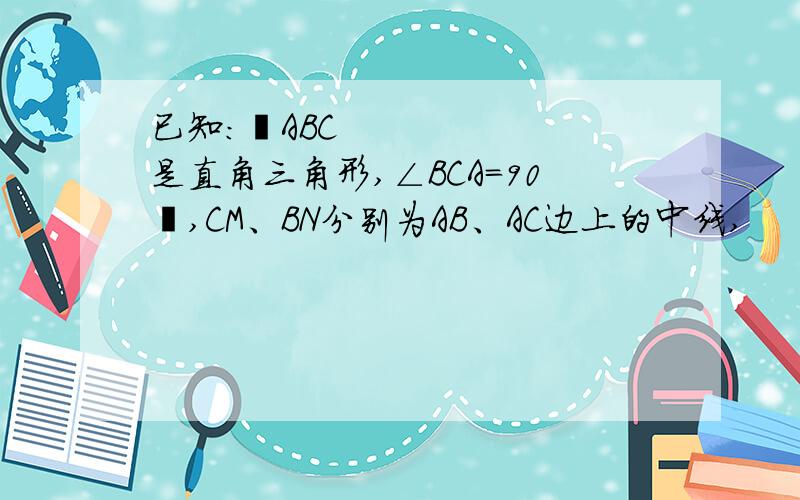
设CM与BN相交于D.
因为∠BCA=90°,CM垂直BN,所以△BCN与△BDC相似,从而有BC²=BD*BN.
因为CM、BN分别为AB、AC边上的中线,所以D是重心,所以BD=2/3 BN.
所以BC²=BD*BN=2/3 BN²,所以BN的长为(√6/2)*a
下面证BD=2/3BN,用中位线定理:做NE//CM,因为N为AC中点,所以AE=EM,又M为AB中点,所以BM=2ME,在△BDM和△BNE中,BD/BN=BM/BE=2/3.

直角三角形ABC中,CD是斜边AB上的中线已知∠B=30°,AC=5cm则AB,CD分别等于多少一道数学题：已知△ABC,AD是角BC边上的中线,分别以AB边、AC边为直角边各向形外做等腰直角三角形, 三角形ABC中,CM、BN是AB、AC上的中线,且CM=BN.求证：AB=AC 如图,ad是△abc中bc边上的中线,已知ab=5cm,ac=3cm,若ab边上的高为2cm,求ac边上的高已知三角形ABC的周长为16cm,AB=AC,AD是BC边上的中线,若BD=3cm,求AB的长如图,已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC,AB所在的直线为x轴,y轴建立直如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,若AB边上的高为2cm,求AC边上的高在Rt△ABC中,∠BCA=90°,中线CM垂直于中线BN,且BC=2,求BN的长已知△ABC,AD是角BC边上的中线,分别以AB边、AC边为直角边各向形外做等腰直角三角形,如图.求证EF=2AD. 在直角三角形abc中,∠acb=90°,cd是ab边上中线,若cd=5cm,则ab=?三角形abc的面积=? 在直角三角形ABC中,CH、CD、CM分别为斜边AB上的高、角ABC平分线、AB边上中线,若角MCD=阿尔法角DCH= 在直角三角形ABC中,∠ABC=90°,CD是AB边上的高,AB=10cm,bc=8cm,ac=6cm