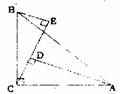
八年级几何题如图,在三角形ABC中,角ABC=90°,AC=BC,BE垂直CE于E,AD垂直CE于D,AD=2.5cm,

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/12 23:41:31

八年级几何题如图,在三角形ABC中,角ABC=90°,AC=BC,BE垂直CE于E,AD垂直CE于D,AD=2.5cm,DE=1.7CM.
如图,在三角形ABC中,角ABC=90°,AC=BC,BE垂直CE于E,AD垂直CE于D,AD=2.5cm,DE=1.7CM.
（1）求BE长
（2）如果过点C在三角形ABC外做一条直线L,分别作AD垂直于L于D,BE垂直于L于E,那么AD,BE,DE之间存在怎样的数量关系?证明你的结论

这个图

有图吗,有的话麻烦在画图工具里画画,比较容易解题!

八年级几何题如图,在三角形ABC中,角ABC=90°,AC=BC,BE垂直CE于E,AD垂直CE于D,AD=2.5cm, 三角形ABC中,角ACB=90°,AC=BC,BE垂直CE于E,AD垂直CE、于D,若AD=2.5cm,DE=1.7cm 如图,在三角形ABC中,角 ACB=90度,AC=BC,BE垂直于CE于点E,AD垂直于CE于如图:在三角形ABC中,角ACB=90度,AC=BC,BE垂直CE,AD垂直CE于D 求证AD=BE+DE 如图,在Rt三角形ABC中,角ACB=90°,AC=BC,BE垂直于CE,AD垂直于CE,垂足分别为E、D,AD=2.6 在三角形ABC中,角ACB=90°,AC=BC,AD垂直于CE,BE垂直于CE,D.E为垂足,试根据三角形全等说明DE+ 如图在三角形ABC中,∠ACB=90度,AC=BC,BE垂直于CE于点E,AD垂直于CE于D,求证AD-BE=DE 在RT△ABC中,角ACB=90度,AC=BC,BE垂直于CE,AD垂直于CE,垂足分别为点E,D,AD=9cm,DE= 如图,在三角形ABC中,AB=AC,AD垂直于BC于D,AD=CB,AD=2CE,CE垂直于BC.求证:BE垂直于AC 如图,在三角形ABC中,∠ACB=90度,AC=BC,CE垂直于BE,CE与AB相交于点F,AD垂直于CF于点D, 如图,在三角形ABC中,角BAC=90°,AD垂直BC于D,CE平分角ACB,交AD于G,交AB于E,EF垂直BC于F. 在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC边的中点,CE垂直于AD,垂足为E,BF平行于AC,交CE的