∑(n=1到∞)(n!)² (2n)!-搜答案-神马作文网

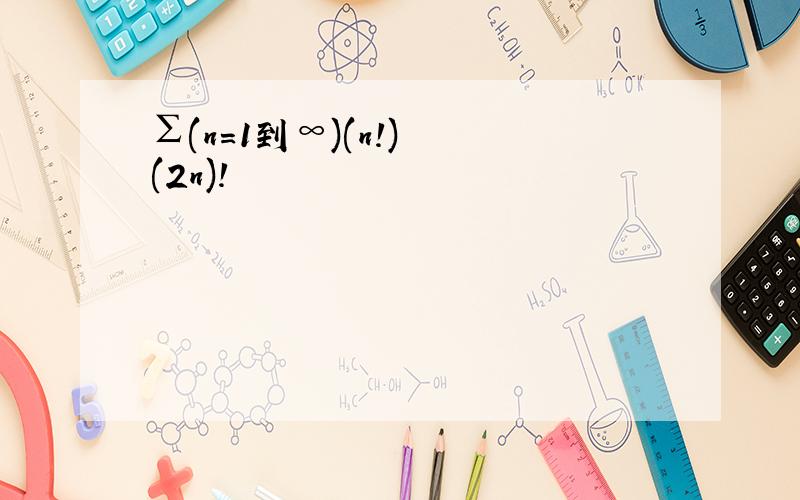
收敛,因为当n充分大的时候,sin(1/n^2)

从第二项开始,n/(n²-2)＞1/n,从1/n发散可以知道该数列发散

n/(2n+1)

S=∑(n=1到∞)[n(n+1)/2]x^(n-1)积分得：F=∑(n=1到∞)[(n+1)/2]x^n再积分得：G=0.5∑(n=1到∞)x^(n+1)=0.5x^2/(1-x)求导得：F=0.5

e^(-x)=1-x/1!+x^2/2!-x^3/3!+...+(-1)^n*x^n/n!+...x∈R即：e^(-1)=1-1/1!+1/2!-1/3!+...+(-1)^n/n!+...=(1/2

使用比值比较法易知幂级数的收敛域为(-1再问：怎么从第二步得到最后结果的？再答：ln(1+x)=x-x^2/2+x^3/3-x^4/4+……ln(1+x²)=x²-(x²

∑(n从1到正无穷)n(n+2)x^n=x∑(n从1到正无穷)n(n+2)x^(n-1)=x∑(n从1到正无穷)[(n+2)x^n]′=x[∑(n从1到正无穷)(n+2)x^n]′∑(n从1到正无穷)

e^(-x^2)（负号在x^2外面）你去看看e^x的幂级数展开,然后作变量代换（因为e^x是在整个实轴上展开的,所以不必担心变量代换以后收敛半径的问题）

记　　f(x)=∑(n=1~inf.)[(n-1)x^(2n-2)]/3^n　=(1/3)∑(n=1~inf.)n[(x^2)/3]^(n-1)-(1/3)∑(n=1~inf.)[(x^2)/3]^(

根据比值判断法,（n+1）项/n项以n趋近于无穷大的比值为1,所以级数可能收敛也可能发散

通项|an|

用莱布尼兹定理呀,可以看出1/(n-lnn)是单减的,这个你可以用构造函数来看,F（x）=1/(x-lnx)求导F（x）再问：当n趋于无穷时，Un为什么=0啊

只需要看后一项与前一项比值【2^n*n!/n^n】/【2^(n-1)*(n-1)!/(n-1)^(n-1)】=2n*(n-1)^(n-1)/n^n=2(n-1)^(n-1)/n^(n-1)=2【(n-

(n+1/n)/(n+1/n)^n开n次根号（柯西判别法）,结果为0,小于1,收敛.且(n+1/n)/(n+1/n)^n恒正,故绝对收敛再问：答案给的是发散，莫非答案错了？

设f(x)=n^(1/x),an=f(n)-f(n+1),有拉格朗日定理,对足够大的n有|an|=f'(ξ)=n^(1/ξ)㏑n/x^2

Σ(n=0~∞)x^n/n!2^n　　=Σ(n=0~∞)(x/2)^n/n!=e^(x/2),-inf.

n从1开始取值啊.收敛域是(0,2].乘以x-1求导,求出和函数后再积分,[(x-1)s(x)]'＝∑(-1)^(n-1)(x-1)^n＝(x-1)∑(1-x)^(n-1)＝(x-1)×1/(1-(1

分子分母同时乘以二化为[∞∑n=1][2^n×x^n]/2(n!),整理[∞∑n=1]﹙2x﹚^n/(n!)×1／2,由公式e^x=[∞∑n=1]x^n/(n!)可得1/2e^2x