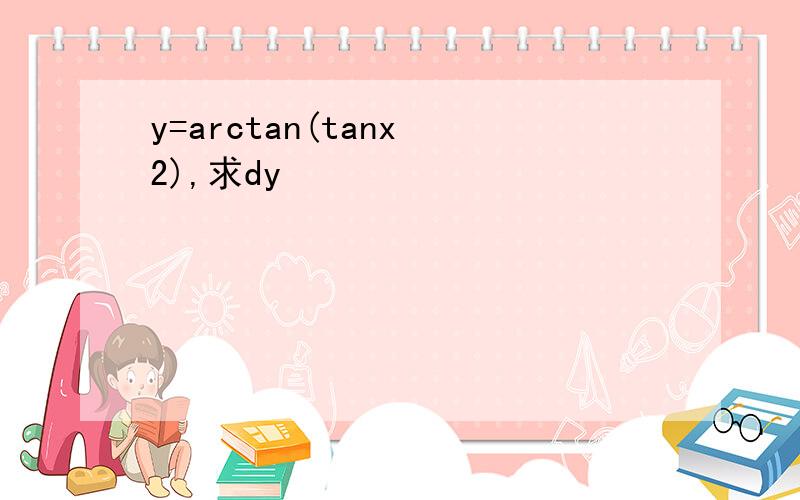
y=arctan(tanx 2),求dy-搜答案-神马作文网

设u=√(y/x)u'x=(-1/2)x^(-3/2)y^(1/2)u'y=(1/2)(xy)^(-1/2)那么原式变成了arctanu=(1/u^2)所以(u^2)arctanu=1两边取全微分得到

首先明确y=arctanx的定义域为R,所以arctan|x|的定义域也为R,至于值域,因为|x|》0,故y应取【0,π/2】

arctan(y)=x+1, y=?

两边取正切y=tan(x+1)

(arctan(1-x^2))'=1/(1+(1-x²)²)(1-x²)’=(-2x)/(1+(1-x²)²)=-2x/(x^4-2x²+2

y=arctanx/(1+x²)那么y'=1/[1+x²/(1+x²)²]*[x/(1+x²)]'=(1+x²)²/[(1+x&#

先求值域√x≥0所以0≤y＜π/2y=arctan√xtany=√xx=tan²y即y=tan^2(x)（0≤x＜π/2)

y=2x*arctan(y/x)y/x=2*arctan(y/x)u=y/xu=2*arctanu两边求解导数dy/dx=2arctan(y/x)+2x*1/((y/x)^2+1)*(1/x*dy/d

f(x)=arctanx的定义域是R;值域是(-π/2,π/2)因为|x|≥0,所以函数f(x)=arctan|x|的定义域为R；值域为[0,π/2)

y=arctan(1-x)1-x=tany对x求导-1=y'sec²y所以y'=-1/sec²y=-cos²y=-cos²[arctan(1-x)]y'=-co

arctan(-2)+arctan(-3)=?

tan[arctan(-2)+arctan(-3)]=-2-3/1-6(用余切公式)=1所以arctan(-2)+arctan(-3)=45度或225度

y'=1/[1+(2tanx/2)²]*(2tanx/2)'=1/[1+(2tanx/2)²]*2sec²(x/2)*(x/2)'=1/[1+(2tanx/2)²

y=arctan(lnx)求导~

对于这样的复合函数,求导就用链式法则,对各个函数逐个求导,在这里y=arctan(lnx),可以令lnx=t,那么y'=(arctant)'*t',显然(arctant)'=1/(1+t²)

arctanx'=1/(1+x^2)y=arctan(x+1)^1/2y'=1/(1+(x+1)^1/2^2)*(x+1)^1/2'y'=1/(x+2)*1/2(x+1)^(-1/2)y'=1/[2(

反函数就是x与y的位置换一下先将其化到最简单,然后将x与y换一下即可y=πarctan(x/2)arctan(x/2)=y/πx/2=tan(y/π)x=2tan(y/π)所以y的反函数为y=2tan

即y/x=2arctan(y/x)令u=y/x,则u=2arctanu这实际是一个关于u的方程,可以证明这个方程是有解的,设u=c是方程的解(这时c已经是一个常数了)即u=y/x=c那么有y=cx所以

y=arctan(1/x)求导

y'=1/[1+(1/x)^2]*(1/x)'=x^2/(1+x^2)*(-1/x^2)=-1/(1+x^2)

差不多,但是有小区别.arctan(x/y)的范围是(-π/2,π/2)而arctan(x,y)的范围是(-π,π]http://www.cplusplus.com/reference/clibrar

y=4arctanxy'=4/(1+x^2)所以y'(1)=4/(1+1^2)=2

y=arctan（x^2+1）

y'=1/[1+(x^2+1)^2]×(x^2+1)'=2x/(x^4+2x^2+2)再问：