f(x,y,z)=-2x^2在x^2-y^2-2z^2=2-搜答案-神马作文网

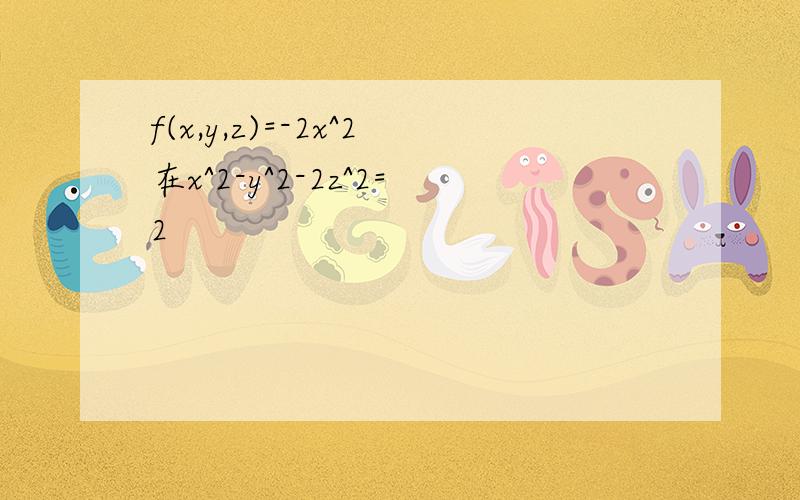
Fx（x,y,z）=2x=2,Fy（x,y,z）=4y=4,Fz（x,y,z）=4z=4,方向余弦分别为cosα=1/3,cosβ=2/3,cosγ=2/3所以方向导数是Fxcosα+Fycosβ+F

dz/dx=y(yf1'+2f2')dz/dy=f(xy,2x+y)++y(xf1'+f2')da/dxdy=(yf1'+2f2')+y【f1'+y(xf1'+f2')+2(xf1'+f2'）】=2y

二重积分,画出积分区域,分段积分就行

有这样的公式：a^3+b^3+c^2-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)左边减右边,证明：（x+y-2z)^3+(y+z-2x)^3+(z+x-2y)^3-3（x+y

1、由单变元的微分中值定理,有f(x,y)－f(x0,y)＝f'x(c,y)*(x－x0)＝0,于是f(x,y)的值只与y有关,故z＝f(y).2、由1知道,当f'xy(x,y)＝0时,f'y(x,y

你的答案正确

%单纯从定义上没有错误,但是如果计算时xyz是数组或向量时就会报错,因为要求加点运算%试改为：f=@(x,y,z)(1+y).*z.^y-(-0.25*(x-1).^2+0.25).^x看看

1.x^2-y^2-2z^2=2x^2=2+y^2+2z^2>=2所以f(x,y,z)=-2x^2

两边对x求导1-a*δz/δx=f'(y-bz)*(-bδz/δx)整理得：[a-bf'(y-bz)]δz/δx=-1两边对y求导-a*δz/δy=f'(y-bz)*(1-bδz/δy)整理得：[-a

如下图不知能看明白否

4zexp(-2z）,z>0

δz/δx=y^2*f1+(2y-1)*f2δz/δy=2xy*f1+x^2y*2*f2再问：f1和f2是什么？再答：f1表示z对x求导，也可写成fx,(x为下标，在右下角，我不好打，不好意思！）这只

把代码补全一点,主要是注意返回类型!#include"stdio.h"intz=5;voidf(){staticintx=2;inty=5;/*x为静态变量,分配了以后直到程序结束,y没实际用到*/x

关键在于将y=2x在求导中按复合函数来处理,首先在f(x,2x)=x两边对x求导数,根据复合函数求导法则,有f'x+f'y*(2x)'=1,即f'x+2f'y=1,由于f'x=x^2,所以f'y=(1

1、隐函数对x求导得1+az/ax+yz+xy*az/ax=0,故az/ax=－(1+yz)/(1+xy)；F对x求导得aF/ax=e^x*y*z^2+e^x*y*2z*az/ax；当x＝0,y＝1时

由柯西不等式,(2^2+1^2+4^2)*(x^2+y^2+z^2)大于等于(2x+y+4z)^2解一下就可以了

z=y/f(x²+y²),令u=x²+y²∂z/∂x=y·-1·[∂f(u)/∂u·∂(x²

=x²(y-z)+y²(z-x)+z²(x-z+z-y)=(y-z)(x²-z²)+(z-x)(y²-z²)=(y-z)(x-z)

f=x+1f+u=2x+3f+u+c=3x+8f+u+c+k=4x+15f(f,u,c,k)=(x+1)(2x+3)(3x+8)(4x+15)

1.用拉格朗日乘数法没有用柯西不等式的方便(x²+y²+z²)*(1+1+1)≥（x+y+z)²=1当x=y=z时等号成立所以x²+y²+z