已知:如图1.3.14,在△ABC中-搜答案-神马作文网

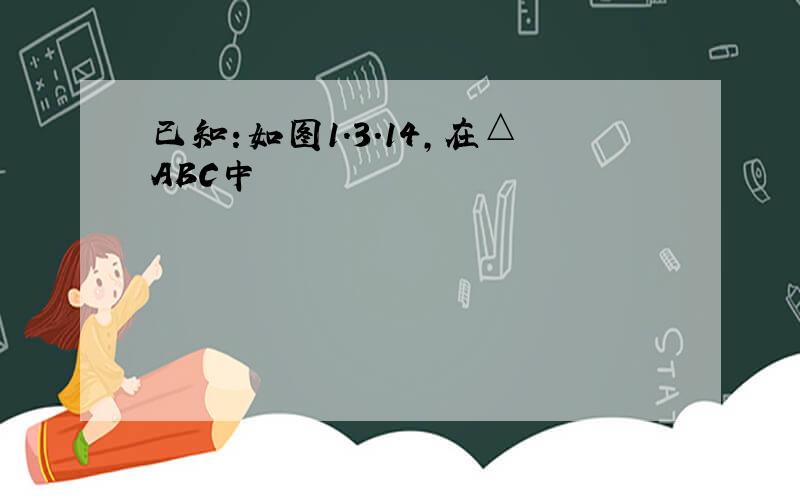
（1）由B（3,m）可知OC=3,BC=m,又△ABC为等腰直角三角形,∴AC=BC=m,OA=m-3,∴点A的坐标是（3-m,0）．（2）∵∠ODA=∠OAD=45°∴OD=OA=m-3,则点D的坐

因为A//C又因为B//C所以A//B做辅助线E垂直于AB证角等

∵AC=8,C△ABE=14, ∴AB+AE+BE=14 ∵DE垂直平分BC &nbs

已知a、b是有理数,在数轴上的位置如图：化简|b|-|a|+|a-b|+|a+b|=-b-a+a-b-a-b=-3b-a

根据数轴可知，a＞0＞b，故原式=-b-a+a-b-a-b=-a-3b．

（1）AC=4,（2）EG=4

因为两个三角形全等,所以角A等于角B,所以AC平行EF；又因为AB等于DF,即AD＋BD等于FB＋BD,所以AD等于BF

过B点作AC的平行线L1过D点作BC的平行线L2,交L1于点G,交AE于J过点E作AC的平行线L3,交L2于点H连接AG交L3于点I则AD=BC=GD,GH=BE=DC=HE那么角AIE=180°-角

过M点在ABC作BC的平行线,交AB于E,交AC于F,连接DE,DF,所得平面DEF即为所求

我估计楼主感觉最难的是直角EAB不知道怎么画!任意画一条直线,在直线上取两点M、N,作线段MN的中垂线（即垂直平分线）,中垂线与MN的交点设为A,中垂线上任取一点设为E,后面的应该没问题了.

证明：在钝角△ABC中，由A+B+C=π，可得sinA=sin（B+C），∴sinA=sinBcosC+cosBsinC，∴2R•sinA=2R•sinBcosC+2R•cosBsinC（R为△ABC

（1）证明：连接OD,∵BC是⊙O的切线,∴OD⊥BC,∵AC⊥BC,∴OD∥AC,∴∠2=∠3；∵OA=OD,∴∠1=∠3,∴∠1=∠2,∴AD平分∠BAC；（2）∵BC与圆相切于点D．∴BD2=B

AB=ACBD=DCAD=AD∴△ABD≌△ACD∴∠1=∠2又AB=ACAM=AM∴△ABM≌△ACM∴MB=MC

这不难（1）∵a,b是方程x^2-(m-1)x+m+4=0的两根∴a+b=m-1①a*b=m+4②∴AB2=52=a2+b2=（a+b）2-2ab=(m-1)2-2（m+4）解得m1=6m2=-2（∵

20°

|a-2|-|a+b|-|b-1|+|a+3|=2-a+(a+b)-(b-1)-(a+3)=2-a+a+b-b+1-a-3=-a

证明：在BC上取一点E,使得CE=AC因为CD=CD,角ACD=角DCE所以三角形ACD全等于三角形ECD所以AD=DE,角A=角DEC因为角DEC=角B+角BDE,角A=2角B所以角B=角BDE所以

三角形的面积公式是S=½ab,P的纵坐标是4,已知面积为4,那就变成2×多少=4,由此可得A的坐标为（2,0）A也为（-1,0）脑子里应该要有概念,可是现在想这道题好累啊.我初一,这道题不难

（1）由已知得DECF是矩形,故EC=DF=y,AE=8-EC=8-y；（2）∵DE∥BC∴△ADE∽△ABC∴∴即y=8-2x（0<x<4）；（3）S=xy=x（8-2x）=-2（x-2

（1）作出CD， &n