2f(xy)f(xy)(ydx xdy)

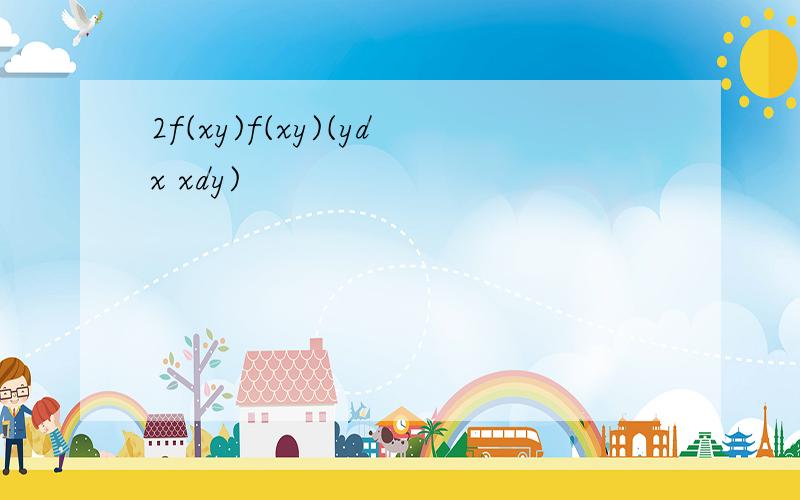
e(-xy)d(-xy)=(xdy+ydx)d(exy^2/2)=d(xy)exy^2=2xy+C,C为任意常数,或x恒等于0,或y恒等于0,或x和y都为常数不知道有没有错呢···

因为f（x+y,xy）=x^2+y^2=（x+y）^2-2xy所以f（x,y）=x^2-2y现对x求导得到：fx(x,y)=2x再对y求导得到：fxy(x,y)=0.所以无论x,y为何值,fxy(x,

f(x,y)={xy/[2-√(4+xy)]=-2-√（4+xy),xy≠0；{4,xy=0,在点(0,0),(1,0)处不连续,在（1,2）处连续.再问：能简述下原因么？再答：f(0+,0+)=-4

f(x+y^2)=f(x)+2[f(y)]^2f(0)=f(0+0^2)=f(0)+2[f(0)]^2f(0)=0f(0+x^2)=f(0)+2[f(x]]^2f(x)=2[f(√x)]^2f(1)=

因为f(8)=3,所以f〔(根号2)的6次方〕=3,6f〔(根号2)〕=3,f(根号2）＝0.5

令x=1,y=1时f(1+1)=f(1)+f(1)=4解得f(1)=2令x=2,y=-1时f(2-1)=f(2)+f(-1)=2解得f(-1)=-2

d(xy)可以理解为xy的一个微小变化量.当x变化微小量dx成为x+dx,y变化微小量dy成为y+dy,所以对应xy（初值）就变化成(x+dx)(y+dy)（末值）,变化量即为末值减初值.再问：三年前

F(8)=F(2*4)=F(2)+F(4)=F(2)+F(2)+F(2)=3F(2)=3所以f(2)=1

证明令x=x/y,y=y∵f(xy)=f(x)+f(y)∴f（x/y*y）=f(x/y)+f(y)f(x)=f(x/y)+f(y)∴f(x/y)=f(x)-f(y)

设a=xy,b=x+y.f(xy,x+y)=x^2+y^2+2xy-2xy=(x+y)^2-2xy把a,b带f(a,b)=b^2-2a所以f(x,y)=y^2-2x同理f(x+y,xy)=x^2+y^

当x=y=0时f(0+0)+f(0)=2f(0)f(0)f(0)²=f(0)f(0)=1或者f(0)=0当y=0时f(x)+f(0)=2f(x)f(0)若f(0)=0f(x)=0若f（0)=

再问：可以再帮我答题吗，我这边有很多财富值可以给你再问：

从题目和问题双方向入手：已知f(1)=2,那么就假设x+y=1,谁是1谁是0没关系,重点是能得到一个新的可知条件f(0)=0,再由此推x+y=0,可以得到f(-x)=2x^2-f(x).此时可以看到,

挺好的题f(xy)=xf(y)+yf(x)---(1)设y=c=常量则：f(cx)=cf(x)+f(c)x两边求导数f'(cx)*c=cf'(x)+f(c)cf'(cx)-cf'(x)=f(c)此式对

∫∫f(u,v)dudv是一个数,记为A,则f(x,y)=xy+A,两边在D上作二重积分,得∫∫f(x,y)dxdy=∫∫xydxdy+A∫∫dxdy即A=∫∫xydxdy+AσA=∫xdx∫ydy+

3=1+1+1=f（2）+f(2)+f(2)=f(2*2)+f(2)=f(4*2)=f(8)f(x)+f(x-2)=f(x*(x-2))=f(x^2-2x)结合定义域知识,所以f(x)+f(x-2)0

定义在R+上的函数f(x)满足f(x)+f(y)+2xy(xy)=f(xy)/f(x+y)对任意x,y∈R+,恒成立,则f（2）=____设x=y=2,则有2f(2)+32=f(4)/f(4)=1,故

x,y都是未知数,你也可以把他们当做t,r那么就是求f（t,r）首先由题意知2x+y=t,2y+x=r用t,r表示x,y,可得x=1/3（2t-r）,y=1/3（2r-t）并将其代入f(2x+y,2y

f(x+y,xy)=x^2+y^2=(x+y)^2-2xyf(x,y)=x^2-2y

答案是0由f(xy)=f(x)+f(y),得f(1)=0,如f(1/4)=f(1)+f(1/4)推出放f(1)=0所以f(1/3)+f(1/2)+f(1)+f(2)+f(3)=f(1/3)+f(3)+