如图,已知抛物线y=ax2+bx+c经过O(0,0)
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/23 17:17:24
如图,已知抛物线y=ax2+bx+c经过O(0,0)
如图,已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,根号3)三点,连结A,B,过点B作BC平行x轴交抛物线于点C.(1)求这条抛物线的函数解析式;
(2)两个懂点P,Q分别从O、A两点同时出发,以每秒1个单位长度的速度运动.其中,点P沿线段OA向A点向A点运动,点Q沿折线A→B→C的路线向C点运动.设这两个动点运动的时间为t(秒)(0<t<4),△PQA的面积记为S.求S与t的函数解析式.
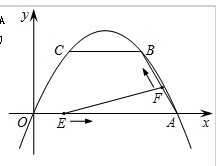
如图,已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,根号3)三点,连结A,B,过点B作BC平行x轴交抛物线于点C.(1)求这条抛物线的函数解析式;
(2)两个懂点P,Q分别从O、A两点同时出发,以每秒1个单位长度的速度运动.其中,点P沿线段OA向A点向A点运动,点Q沿折线A→B→C的路线向C点运动.设这两个动点运动的时间为t(秒)(0<t<4),△PQA的面积记为S.求S与t的函数解析式.


(1)
经过O,A(4,0),可表达为y = ax(x - 4)
经过B(3,√3):-3a = √3
a = -√3/3,b = 4√3/3
抛物线的函数解析式:y = -√3/3(x² - 4x)
(2)
t秒时:P(t,0)
(i) Q在AB上
AB的解析式:(y - 0)/(√3 - 0) = (x - 4)/(3 - 4),y = -√3(x - 4)
AB = √[(3 - 4)² + (√3 - 0)²] = 2
0 < t < 2
设Q(q,-√3(q - 4)),显然0 < q < 4
AQ² = OP² = t² = (q - 4)² + [-√3(q - 4) - 0]² = 4(q - 4)²
q = 4 - t/2 (舍去q = 4 + t/2)
Q(4 - t/2,√3t/2)
S = (1/2)PA*Q的纵坐标 = (1/2)(4 - t)*√3t/2 = √3(4 - t)t/4
(ii)Q在BC上
2 < t < 4
QB = t - AB = t - 2,Q的横坐标 = B的横坐标 - QB = 3 - (t - 2) = 5 - t
Q(5 - t,√3)
S = (1/2)PA*Q的纵坐标 = (1/2)(4 - t)√3 = √3(4 - t)/2
经过O,A(4,0),可表达为y = ax(x - 4)
经过B(3,√3):-3a = √3
a = -√3/3,b = 4√3/3
抛物线的函数解析式:y = -√3/3(x² - 4x)
(2)
t秒时:P(t,0)
(i) Q在AB上
AB的解析式:(y - 0)/(√3 - 0) = (x - 4)/(3 - 4),y = -√3(x - 4)
AB = √[(3 - 4)² + (√3 - 0)²] = 2
0 < t < 2
设Q(q,-√3(q - 4)),显然0 < q < 4
AQ² = OP² = t² = (q - 4)² + [-√3(q - 4) - 0]² = 4(q - 4)²
q = 4 - t/2 (舍去q = 4 + t/2)
Q(4 - t/2,√3t/2)
S = (1/2)PA*Q的纵坐标 = (1/2)(4 - t)*√3t/2 = √3(4 - t)t/4
(ii)Q在BC上
2 < t < 4
QB = t - AB = t - 2,Q的横坐标 = B的横坐标 - QB = 3 - (t - 2) = 5 - t
Q(5 - t,√3)
S = (1/2)PA*Q的纵坐标 = (1/2)(4 - t)√3 = √3(4 - t)/2
如图,已知抛物线y=ax2+bx+c经过O(0,0)
已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
已知,如图,抛物线y=ax2+bx+c经过点A(-1,0),B(0,-3),C(3,0 )三点.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(-3,0)
已知抛物线y=ax2+bx+c,经过(0,1)和(2,-3)两点.
(2012•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的图象经过原点O,交x轴于点A,其顶点B的坐标为(3,-
如图1,已知在平面直角坐标系中,抛物线y=ax2 bx c经过A(-1,0)B(3,0)两点,且
如图1,已知抛物线y=ax2+bx(a不=0)经过A(3,0
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,3)三点.
如图已知经过原点的抛物线y=ax2+bx(a不等于0)经过A(-2,2),B(6,6)两点已知过原点的抛物线y=ax2+
已知抛物线y=ax2+bx+c
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交