神马作文网2、3小题
来源：学生作业帮 编辑：神马作文网作业帮 分类：数学作业 时间：2024/11/23 19:16:59
解题思路： 关键是用字母表示出EF的坐标，代入y=k/X中，得出k的值，从而求出解析式
解题过程：
（2）设反比例函数为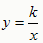
，点E和F在该比例函数图像上，
设F（E，2），则E（E＋3，1）
把点F'和E的坐标分别代入，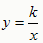
得k＝2E；k＝E＋3，
∴2E＝E＋3，E＝3，则k＝6，
反比例函数解析式为
。
得点F（3，2）；E（6，1）。
设直线FE的解析式为y＝ax＋b，把F、E两点坐标代入
得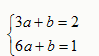
∴解
之得：
；
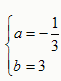∴直线FE的解析式为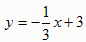
。
（3）设EF与y轴的交点是G，Q是 GF的中点，由G（0，3），F（3，2），
得点Q的横坐标为
，点Q的纵坐标为2＋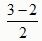
＝
，
∴Q（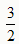
，
）
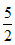过点Q作直线l与x轴交于M'点，与的图象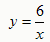
交于P'点，
若四边形P'G M' F是平行四边形，则有P'Q＝Q M'，
易知点M'的横坐标大于
，点P'的横坐标小于
作P'Ｈ⊥x轴于点H，QK
⊥y轴于点K，P'H与QK交于点O，
作QF⊥x轴于点F，则△P'OQ≌△QZM'
设OQ＝ZM'＝t，则点P'的横坐标x为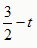
，点P'的纵坐标y为
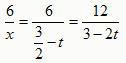，点M'的坐标是（
，0）
∴P'O＝
。
由P'Q＝QM'，得P'E2＋EQ2＝QF2＋FM'2，
∴
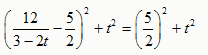
整理得：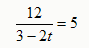
，解得
（经检验，它是分式方程的解）
∴
；
；
。
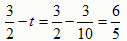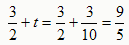得P'（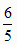
，5），M'（
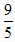，0），则点P'为所求的点P，点M'为所求的点M。
解题过程：
（2）设反比例函数为
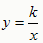，点E和F在该比例函数图像上，设F（E，2），则E（E＋3，1）
把点F'和E的坐标分别代入
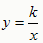，得k＝2E；k＝E＋3，
∴2E＝E＋3，E＝3，则k＝6，
反比例函数解析式为
。得点F（3，2）；E（6，1）。
设直线FE的解析式为y＝ax＋b，把F、E两点坐标代入
得
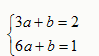
∴解
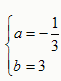之得：；∴直线FE的解析式为
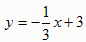。（3）设EF与y轴的交点是G，Q是 GF的中点，由G（0，3），F（3，2），
得点Q的横坐标为
，点Q的纵坐标为2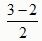＋＝，∴Q（
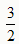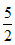，）过点Q作直线l与x轴交于M'点，与的图象
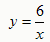交于P'点， 若四边形P'G M' F是平行四边形，则有P'Q＝Q M'，
易知点M'的横坐标大于
，点P'的横坐标小于作P'Ｈ⊥x轴于点H，QK
⊥y轴于点K，P'H与QK交于点O，作QF⊥x轴于点F，则△P'OQ≌△QZM'
设OQ＝ZM'＝t，则点P'的横坐标x为
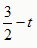，点P'的纵坐标y为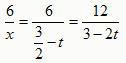，点M'的坐标是（，0）∴P'O＝
。 由P'Q＝QM'，得P'E2＋EQ2＝QF2＋FM'2，
∴
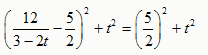
整理得：
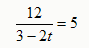，解得（经检验，它是分式方程的解） ∴
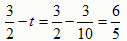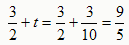；；。得P'（
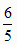，5），M'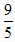（，0），则点P'为所求的点P，点M'为所求的点M。