sin50°sin37°+sin122°sin53°=?
来源:学生作业帮 编辑:神马作文网作业帮 分类:物理作业 时间:2024/11/18 07:55:09
sin50°sin37°+sin122°sin53°=?
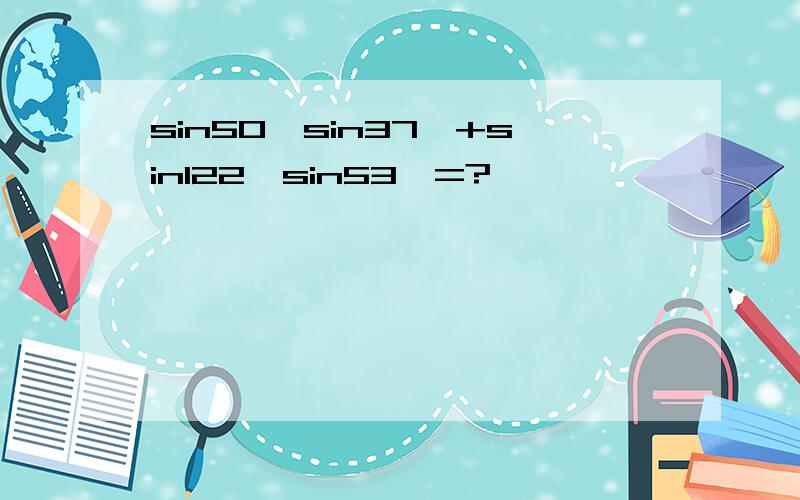
sin50°sin37°+sin122°sin53°
=sin50°sin37°+sin(90°+32°)sin(90°-37°)
=sin50°sin37°+cos32°cos37°
因此题中的四个角应该修改以便于应用两角和与差的三角公式.
解决这类问题的关键在于观察所给角之间的数量关系,若是两个不同的角且符合sinacosb+cosasinb或sinacosb-cosasinb或cosacosb+sinasinb或cosacosb-sinasinb结构,那么就可以直接利用公式解决;若是几个不同的角,那么就要研究这几个角之间的关系是否互补或互余,如是互补或互余的关系那么就可以利用诱导公式将所给的角转化为2个角然后应用两角和与差的三角公式解决即可.
再问: 如果是sin58°sin27°+sin122°sin53°改怎么变换
再答: 因58°+122°=180°,27°+53°=80°,故 sin58°sin27°+sin122°sin53° =sin58°sin27°+sin(180°-58°)sin(80°-27°) 它的结构与两角和与差的三角公式不符,还是不能利用公式计算。但若把sin122°改成cos122°,27°改成37°,那么问题就可解决如下: sin58°sin37°+cos122°sin53° =sin58°sin37°+cos(180°-58°)sin(90°-37°) =sin58°sin37°-cos58°cos37° =-cos(58°+37°) =-cos95°
再问: sin122°=cos122°? 怎么来的
再答: 没有算式sin122°=cos122°。实际上cos122°=cos(180°-58°)
=sin50°sin37°+sin(90°+32°)sin(90°-37°)
=sin50°sin37°+cos32°cos37°
因此题中的四个角应该修改以便于应用两角和与差的三角公式.
解决这类问题的关键在于观察所给角之间的数量关系,若是两个不同的角且符合sinacosb+cosasinb或sinacosb-cosasinb或cosacosb+sinasinb或cosacosb-sinasinb结构,那么就可以直接利用公式解决;若是几个不同的角,那么就要研究这几个角之间的关系是否互补或互余,如是互补或互余的关系那么就可以利用诱导公式将所给的角转化为2个角然后应用两角和与差的三角公式解决即可.
再问: 如果是sin58°sin27°+sin122°sin53°改怎么变换
再答: 因58°+122°=180°,27°+53°=80°,故 sin58°sin27°+sin122°sin53° =sin58°sin27°+sin(180°-58°)sin(80°-27°) 它的结构与两角和与差的三角公式不符,还是不能利用公式计算。但若把sin122°改成cos122°,27°改成37°,那么问题就可解决如下: sin58°sin37°+cos122°sin53° =sin58°sin37°+cos(180°-58°)sin(90°-37°) =sin58°sin37°-cos58°cos37° =-cos(58°+37°) =-cos95°
再问: sin122°=cos122°? 怎么来的
再答: 没有算式sin122°=cos122°。实际上cos122°=cos(180°-58°)
为什么sin50°=cos40°
sin10°sin50°-sin50°sin70°-sin70°sin10°=?
sin10°sin30°sin50°sin70°=?
sin50°=a cos40°=?cos50°?
2sin50°(1+根号3tan10°)=?
sin50°(1+√3tan10°)=
sin50°(1+(根号3)tan10°)=
sin50°(1+根号3tan10°)
计算1sin50°+3cos50°
化简sin50°(1+3tan10°)
高中数学化简题sin50°(1+根号3)=
数学卷五一(2):sin23°×cos37°+cos23°×sin37°=( ).求详解,