如图，AB是⊙O的直径，CD切⊙O于E，AC⊥CD于C，BD⊥CD于D，交⊙O于F，连接AE、EF．

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/13 10:43:35

（1）求证：AE是∠BAC的平分线；
（2）若∠ABD=60°，则AB与EF是否平行？请说明理由．

如图，AB是⊙O的直径，CD切⊙O于E，AC⊥CD于C，BD⊥CD于D，交⊙O于F，连接AE、EF．

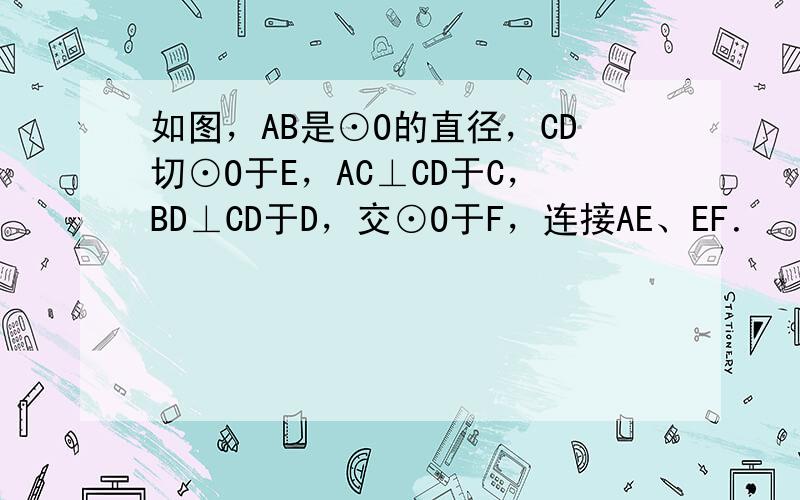
（1）证明：连接BE；
∵AB是⊙O的直径，
∴∠AEB=90°．
∵CD切圆于E，
∴∠AEC=∠ABE，又AC⊥CD．
∴∠CAE=∠BAE．
即AE是∠BAC的平分线．
（2）AB∥EF．理由如下：
∵AC⊥CD于C，BD⊥CD于D，
∴AC∥BD．
∴∠BAC=180°-∠B=120°．
∵AE是∠BAC的平分线，
∴∠BAE=60°．
∴∠DFE=∠BAE=60°（圆内接四边形的任意一个外角等于它的内对角），
∴∠DFE=∠ABF．
∴AB∥EF．

如图,△ABC内接于⊙O,AB是⊙O的直径,CD平分∠ACB交⊙O于点D,交AB于点F,弦AE⊥CD于点H,连接CE、O 如图，AB为⊙O的直径，CD⊥AB于点E，交⊙O于点D，OF⊥AC于点F．如图,△ABC内接于⊙O,CD⊥AB于P,交⊙O于D,E为AC的中点,EP交BD于F,⊙O的直径为d.下列结论:&nbs 如图AB是⊙O的直径弦CD⊥AB于P 如果弦AE交CD于F,求证AC²=AF×AE 如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD=10，连接BD．如图,AB为圆O的直径,CD⊥AB于点E,交圆O于C、D两点,OF⊥AC于点F 如图,已知AB是⊙O的直径,CD⊥AB,垂足为D,AE⊥AB,且AE=AC,BE交圆O于点F 求证：EF·EB=AD·A 如图，AB是圆O的直径，CD⊥AB于D，且AD=2BD，E为AD的中点，连接CE并延长交圆O于F．若CD=2，则AB= 在⊙O中,AB是直径,CD是弦,CE⊥CD于点C,交AB于点E,DF⊥CD于点D,交AB于点F求证：AE=BF 如图，已知A、B、C、D是⊙O上的四个点，AB=BC，BD交AC于点E，连接CD、AD．如图,△ABC中,AC=6,BC=4,以AB为直径的⊙O经过点C,CD平分∠ACB交⊙O于点D,AE⊥CD于点E,则OE 如图,AB是圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F.