fx=sin(2x+π/6)+sin(2x-π/6)+2(cosx)^2 （x∈R）

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/18 01:43:10

fx=sin(2x+π/6)+sin(2x-π/6)+2(cosx)^2 （x∈R）
1.求fx的最大值及此时x的取值集合
2.求fx的单调增区间
3.求y=sinx的图象经过怎样的变化得到fx

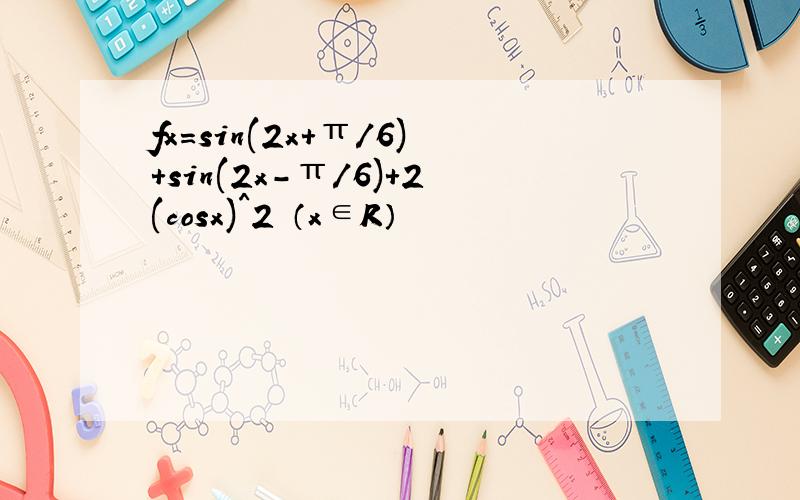
1.用两角和与差的正弦公式展开化简得
　　　　f(x)=√3sin2x+1+cos2x=2sin(2x+π/6)+1,由此得2x+π/6=2kπ+π/2时,f(x)最大值为3,此时x的取值范围是｛x∈R｜x=kπ+π/6,k∈Z｝.
以下两问只说结论了,符号太难打了
2.f(x)的单调增区间是[kπ-π/3,kπ+π/6],k∈Z.
3.可将y=sinx的图像向左平移π/6单位,再将所得图像各点纵坐标不变,横坐标变为原来的一半,然后将所得图像各点横坐标不变,纵坐标变为原来的2倍,最后再将所得图像各点向上平移11个单位得函数f(x)的图像.

已知函数fx=2sin(π-x)cosx 已知函数fx=[cosx+cos(π/2-x)][cosx+sin(π+x)] 函数y=2sin(π/6-x)+2cosx（x∈R)的最小值已知函数fx=sin（2x+π/6）+sin（2x-π/6）+2cos^2x（x属于R）函数f(x)=[2sin(x+π/3)+sinx]cosx-根3sin^2x,(x∈R). 已知函数f(x)=[2sin(x+π/3)+sinx]cosx-√3sin²x,x∈R 化简函数fx=sin(2x+π/6)+2sin^2x 已知函数fx =2sin(x-6分之派 )cosx+2cos平方x 已知sin(π/2-x)=-2sin(π+x),x∈R,则sinx·cosx= 利用cosx=sin(π/2-x),sin'x=cosx,证明(cosx)'=-sinx 已知f（x） =sin（2x+π/6）+3/2,x∈R.求函数fx的单调减区间已知函数fx=（1+1/tanx）sin^x-2sin（x+π/4)sin（x-π/4）