∫(sinx)^4×(cosx)^2dx
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/18 21:21:44
∫(sinx)^4×(cosx)^2dx
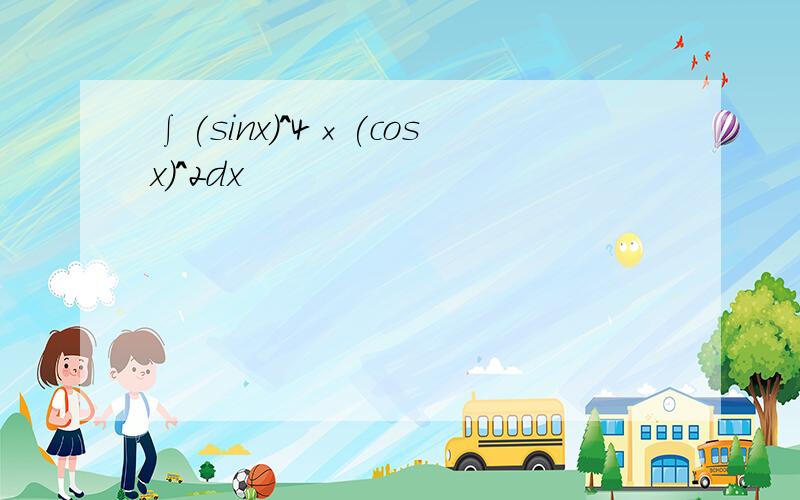
∫(sinx)^4*(cosx)^2*dx (线分部积分)
=-1/3*(cos x)^3*(sinx)^3+∫(cos x)^4*(sinx)^2*dx
∫(cos x)^4*(sinx)^2*dx
当x=pi/2-t时有
∫(cos x)^4*(sinx)^2*dx =-∫(cos ((pi/2-x))^4*(sin(pi/2-x))^2*dx
=-∫(sinx)^4*(cosx)^2*dx
∴∫(sinx)^4*(cosx)^2*dx
=-1/3*(cos x)^3*(sinx)^3+∫(cos x)^4*(sinx)^2*dx
=-1/3*(cos x)^3*(sinx)^3-∫(sinx)^4*(cosx)^2*dx
∴
2*∫(sinx)^4*(cosx)^2*dx =-1/3*(cos x)^3*(sinx)^3
∫(sinx)^4*(cosx)^2*dx =-1/6*(cos x)^3*(sinx)^3+C
=-1/3*(cos x)^3*(sinx)^3+∫(cos x)^4*(sinx)^2*dx
∫(cos x)^4*(sinx)^2*dx
当x=pi/2-t时有
∫(cos x)^4*(sinx)^2*dx =-∫(cos ((pi/2-x))^4*(sin(pi/2-x))^2*dx
=-∫(sinx)^4*(cosx)^2*dx
∴∫(sinx)^4*(cosx)^2*dx
=-1/3*(cos x)^3*(sinx)^3+∫(cos x)^4*(sinx)^2*dx
=-1/3*(cos x)^3*(sinx)^3-∫(sinx)^4*(cosx)^2*dx
∴
2*∫(sinx)^4*(cosx)^2*dx =-1/3*(cos x)^3*(sinx)^3
∫(sinx)^4*(cosx)^2*dx =-1/6*(cos x)^3*(sinx)^3+C