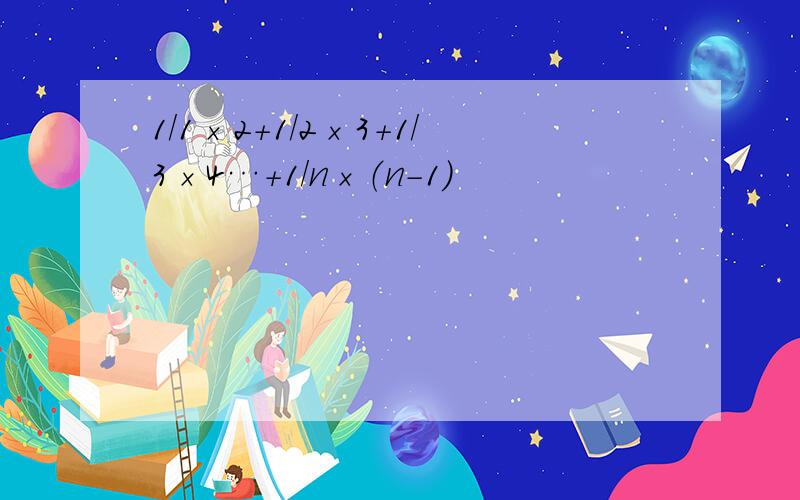1/1×2＋1/2×3＋1/3×4…＋1/n×（n－1）

若n为正整数,求1/n(n+1)+1/(n+1)(n+2)＋1/(n+2)(n+3)+1/(n+3)(n+4)+.+1/ 证明不等式：(1/n)^n+(2/n)^n+(3/n)^n+.+(n/n)^n 化简整式.六分之一× [ 3n×（n＋1）＋2n×（n＋1）×（n－1)] (1/(n^2 n 1 ) 2/(n^2 n 2) 3/(n^2 n 3) ……n/(n^2 n n)) 当N越于无穷大 化简：1/(n+1)(n+2)+1/(n+2)(n+3)+1/(n+3)(n+4) (n+1)(n+2)/1 +(n+2)(n+3)/1 +(n+3)(n+4)/1 lim（√n^2＋1＋√n）/^4√n^3＋n-n（n→∞） n分之1＋n分之2+n分之3+……n分之n-1= [3n(n+1)+n(n+1)(2n+1)]/6+n(n+2)化简 用数学归纳法证明：1×2×3+2×3×4+…+n×(n+1)×(n+2)＝n(n+1)(n+2)(n+3)4(n∈N lim(1/n^2+4/n^2+7/n^2+…+3n-1/n^2) 化简(n+1)(n+2)(n+3)