已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针
来源:学生作业帮 编辑:神马作文网作业帮 分类:综合作业 时间:2024/11/17 15:09:01
已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,试证:①△ABD≌△ACF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中AC=CF+CD的结论是否仍然成立?若成立,请说明理由,若不成立,请写出AC、CF、CD之间存在的数量关系,并证明你的结论;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.

(1)如图1,当点D在边BC上时,试证:①△ABD≌△ACF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中AC=CF+CD的结论是否仍然成立?若成立,请说明理由,若不成立,请写出AC、CF、CD之间存在的数量关系,并证明你的结论;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.

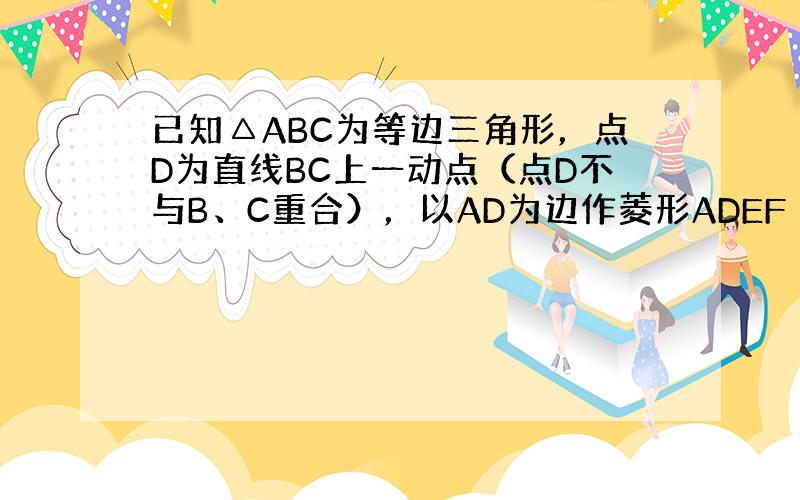
(1)证明:∵四边形AFED是菱形,
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
∵在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴CF+CD=BD+CD=BC=AC,
∴AC=CF+CD.
(2)AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD,
理由是:由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF,
在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴CF-CD=BD-CD=BC=AC,
即AC=CF-CD.

(3)AC=CD-CF.
证明:∵四边形AFED是菱形,
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∵BC=CD-BD,
∴BC=CD-CF.
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
∵在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴CF+CD=BD+CD=BC=AC,
∴AC=CF+CD.
(2)AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF-CD,
理由是:由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,即∠BAD=∠CAF,
在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴CF-CD=BD-CD=BC=AC,
即AC=CF-CD.

(3)AC=CD-CF.
证明:∵四边形AFED是菱形,
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
在△BAD和△CAF中,
AB=AC
∠BAD=∠CAF
AD=AF,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∵BC=CD-BD,
∴BC=CD-CF.
已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,
已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合),AB为边作菱形ADEF,∠DAF=60°,连接C
已知:在三角形ABC中,角ACB为锐角,D是射线BC上的一动点(D与C不重合),以AD为一边向右侧作等边三角形(C与E不
已知:在△ABC中,∠ACB为锐角,D是射线BC上一动点(D与C不重合).以AD为一边向右侧作等边△ADE(C与E不重合
已知:三角形ABC是边长为1的等边三角形,D是射线BC上的一个动点(与点B、C不重合),以AD为一边向右侧作等边三角形A
在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD于点E,交直线AC于点F
如图,过△ABC的顶点A作AE⊥BC,垂足为E.点D是射线AE上一动点(点D不与顶点A重合),连结DB、DC.已知BC=
在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠D
三角形ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),三角形ADE是以AD为边的等边三角形,过点
请教一道数学题:如图, 已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M为直线BC上一动点
关于函数的三角形如图,△ABC是等边三角形,AB=4,D点是AB边的一动点(不与A,B重合),过D点作DE⊥BC于E,过
如图,已知等边三角形ABC中,点D、E、F分别为AB、AC、BC边的中点,M为直线BC上一动点,△DMN为等边三角形(点