作业帮 > 数学 > 作业

如图，在△ABC中，点O是AC边上的一个动点，过点O作MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F

来源：学生作业帮 编辑：神马作文网作业帮 分类：数学作业 时间：2024/11/12 23:13:32
如图，在△ABC中，点O是AC边上的一个动点，过点O作MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OC=
1
2
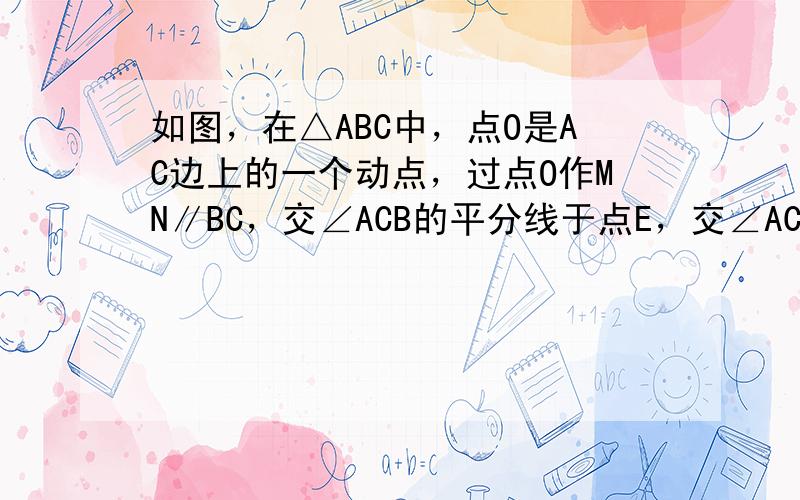
如图，在△ABC中，点O是AC边上的一个动点，过点O作MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F
证明：（1）∵CE平分∠ACB，
∴∠BCE=∠OCE，
∵MN∥BC，
∴∠BCE=∠OEC，
∴∠OEC=∠OCE，
∴OE=OC，
同理，OC=OF，
∴OC=OE=OF，
故0C=
1
2EF；
（2）当点O位于AC边的中点时，四边形AECF是矩形．
由（1）知OE=OF，
又O为AC边的中点，
∴OA=OC，
∴四边形AECF是平行四边形，
∵∠ECO=
1
2∠ACB，∠OCF=
1
2∠ACD，
∴∠ECF=∠ECO+∠OCF=
1
2（∠ACB+∠ACD）=90°，
∴四边形AECF是矩形．
如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内 如图,在△ABC中,点O是AC边上的一个动点,过O点作直线MN‖BC,设MN交∠BCA的平分线于点E,交∠ACD的外角平 如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分 如图 △ABC中 点O是AC边上的一个动点 过点O作直线MN‖BC 设MN交∠BCA的平分线于E 交∠BCA的外角平分线 在△ABC中,点O是AC边上的一个动点,过点O作直线MN‖BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线 如图,在三角形ABC中,点O是AC边上的一个动点,过点O做直线MN平行BC,交∠ACB的平行线于点E,交∠ACB的外角 在△ABC中,点O是AC边上的一个动点,过O点作直线MN‖BC,MN交∠BCA的平分线CE于点E,交∠BCA的外角∠AC 如图,三角形ABC中,点O是AC边上一个动点,过点O作直线MN//BC,设MN交∠BCA的平分线于E,交∠BCA的外角平 如图,在三角形ABC中,点O是AC边上的一个动点,过点O作直线MN平行于BC,设MN交∠BCA的角平分线于点E,交∠BC 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC．设MN交∠BCA的平分线于点E. 如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN‖BC,设MN交角BCA的平分线于点E,交△ABC的外角角A