1.y'=x(1-y^2)^(1/2).求y 2.(x^2-9)y'+xy=0,y(5)=1.求y

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/12 00:09:59

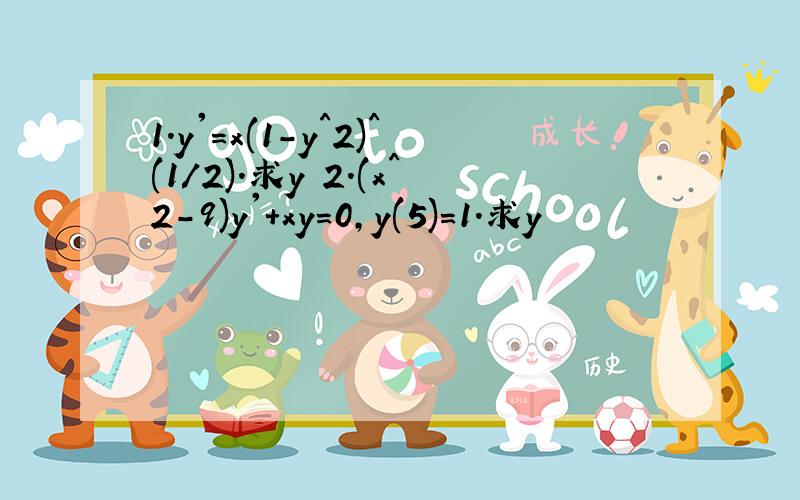
解微分方程：1.y'=x√(1-y²)；求y 2.(x^2-9)y'+xy=0,y(5)=1.求y
1.dy/dx=x√(1-y²)
分离变量得 dy/√(1-y²)=xdx,两边分别积分之得 arcsiny=(1/2)x²+C；即y=sin[(1/2)x²+C]为
其通解.
2.(x²-9)y'+xy=0,y(5)=1；
(x²-9)(dy/dx)=-xy,分离变量得：(1/y)dy=-xdx/(x²-9)；即有(1/y)dy=-(1/2)d(x²-9)/(x²-9)
积分之,得lny=-(1/2)ln(x²-9)+lnC,故通解为 y=C/√(x²-9)；用y(5)=1代入得1=C/√(25-9)
故C=4,于是特解为 y=4/√(x²-9).

已知x+y=-1,xy=-2,求代数式-5（x+y)+(x-y)+x(xy+y)的值已知x+y=-1,xy=-2,求代数式-5（x+y)+(x-y)+2(xy+y)的值已知X+Y=-1,xy=-2,求代数式-5(x+y)+(x-y)+(xy+y)的值已知x*x-4xy+4y*y=0 求[2x(x+y)-y(x+y)]/(4x*x-4xy+y*y)的值? 已知实数x,y满足x²+y²-xy+2x-y+1=0 求x y 若(x*x+y*y)(x*x+y*y)-4x*x*y*y=0,求代数式(x*x+5xy+y*y)/(x*x+2xy+y* x+y=1,xy=-1/2,求x(x+y)(x-y)-x(x+y)2 已知1/x+1/y=5,求2x-3y+2y/-x+2xy-y 已知1/x+1/y=5,求(2x-3y+2y)/(x+2xy+y)的值 1.若x分之1-y分之1=2,则求x-xy-y分之3x+xy-3y=0的值.2.设x,y为实数,且x-y=3.求x乘根号 1/x-1/y=3,求2x+3xy-2y/x-y 已知x,y>0 2x+y+3=xy 求5x+4y最小值