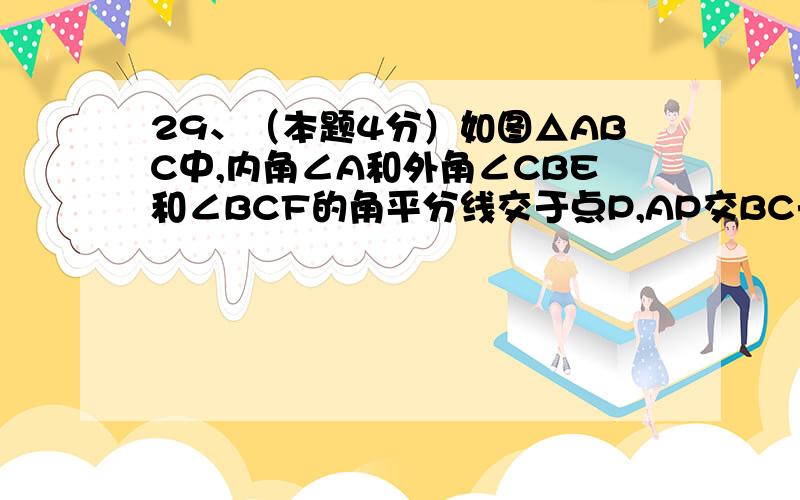
29、（本题4分）如图△ABC中,内角∠A和外角∠CBE和∠BCF的角平分线交于点P,AP交BC于D.过B作BG⊥AP于

来源：学生作业帮编辑：神马作文网作业帮分类：数学作业时间：2024/11/19 07:10:18

29、（本题4分）如图△ABC中,内角∠A和外角∠CBE和∠BCF的角平分线交于点P,AP交BC于D.过B作BG⊥AP于G
(1) 若∠GBP=45º,求证：AC⊥BC；
(2) 在图上作出△PDC在PC边的高DH,并探究∠APB和∠HDC的数量关系,并说明理由；

我来试试.
1)
根据题意,有:
∠BAP=∠CAP,∠CBP=∠EBP,∠BCP=FCP
设∠BAP=∠CAP=∠1,∠BCP=FCP=∠2,∠CBP=∠EBP=∠3
显然:2∠3=2∠1+(180度-2∠2),简化后得到:∠2+∠3-∠1=90度.(1)
∵∠GBP=45度,但是BG⊥AP
∴∠GPB=45度
从而有,∠GPB+∠1=∠3,即∠3-∠1=∠GPB=45度.(2)
结合(1)和(2)可得:∠2+45度=90度,即∠2=45度
∵∠2=45度
∴∠BCP=FCP=∠2=45度,即∠BCF=90度,BC⊥CF
∵F在AC的延长向上
∴BC⊥AC
2)
∵∠GPB=∠3-∠1,∠HDC=90度-∠2
∴∠GPB-∠HDC=∠3-∠1-90度+∠2=(∠2+∠3-∠1)-90度=0
即:∠GPB=∠HDC

如图,在△ABC中,P是AC上的一个动点,过点P作直线EF‖BC,EF交∠ABC的平分线于点D,交其外角的平分线于点D, △ABC的外角平分线BP和CP交于点P,试证明：AP平分∠BAC 如图11-3.2-7,△ABC的外角平分线BP和CP交于点P,试证明:AP平分∠BAC 如图,已知△ABC的两个外角平分线BP与CP交于P点,连AP.求证:AP平分∠BAC 如图,△ABC中,∠ABC和∠ACB的平分线交于F点,过点F作DE‖BC交AB于D,交AC于E,AB＝6,AC=4,BC 如图2,若三角形abc中∠b的平分线bo与∠abc的外角平分线co交于o,过o点作ef平行bc交ab于f,ef和be,c 已知,如图①所示,在△ABC中,已知∠B和∠C的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.求证：如图,已知：AP,CP分别是△ABC的外角∠MAC与∠NCA的平分线它们交于P,PD⊥BM于D,PF⊥BN于F.求证：B Z已知如图CE是RT△ABC的斜边AB上的高,在CE的延长线上任取一点P,连接AP,过点B作BG⊥AP于点G,并交CP于已知,三角形ABC的外角平分线BP、CP交于P点,连接AP.求证：AP平分∠BAC. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于如图,在△ABC中,∠B的平分线与∠C的外角平分线相交于点D,DG//BC交AC、AB于F、G两点,求证：GF=BG-C