等腰三角形ABC的底角∠B=36°,D是底边BC上的点,且BD=AD.判断D是不是线段BC的黄金分割点,并说明理%
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/19 04:10:59
等腰三角形ABC的底角∠B=36°,D是底边BC上的点,且BD=AD.判断D是不是线段BC的黄金分割点,并说明理%
等腰三角形ABC的底角∠B=36°,D是底边BC上的点,且BD=AD.判断D是不是线段BC的的黄金分割点,并说明理由
等腰三角形ABC的底角∠B=36°,D是底边BC上的点,且BD=AD.判断D是不是线段BC的的黄金分割点,并说明理由
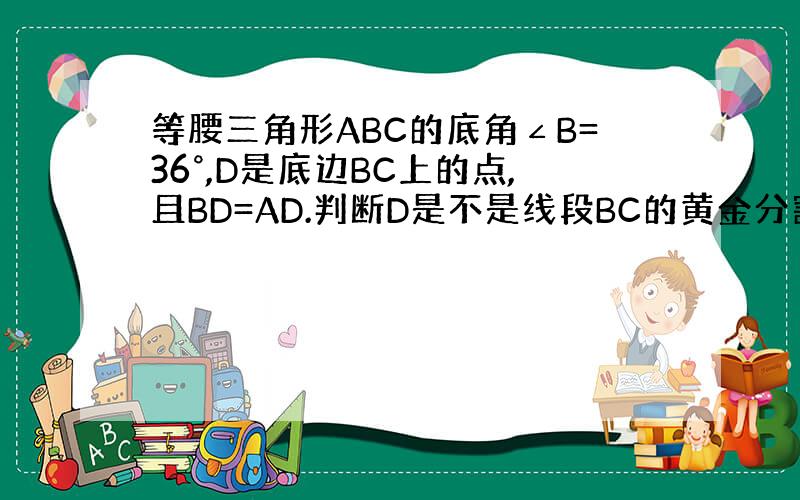
是.
理由:因为AB=AC,所以∠B=∠C=36°,又因为BD=AD,所以∠B=∠BAD=36°,
∠BAC=∠ADB=108°,所以∠ADC=∠DAC=72°,所以AC=DC=AB,
因为∠B=∠C,∠BAD=∠B,所以△DAB∽△ABC,所以BD/AC=AB/BC,
即是BD/DC=DC/BC,所以D是BC的黄金分割点.
理由:因为AB=AC,所以∠B=∠C=36°,又因为BD=AD,所以∠B=∠BAD=36°,
∠BAC=∠ADB=108°,所以∠ADC=∠DAC=72°,所以AC=DC=AB,
因为∠B=∠C,∠BAD=∠B,所以△DAB∽△ABC,所以BD/AC=AB/BC,
即是BD/DC=DC/BC,所以D是BC的黄金分割点.
如图,已知△ABC中,D在BC上,且AB=BD=AC,AD=CD.(1)求∠B(2)证明:D是线段BC的黄金分割点.
如图AD是等腰三角形ABC的底边BC的中线,点EF分别在AB,AC上,且AE=AF,请问点EF关于直线AD对称吗并说明理
等腰三角形ABC中,顶角∠A=36度,底角的平分线BD交AC于D,得D是线段AC的黄金分割点,若AC=10厘米,求AD的
已知D是等腰三角形ABC底边BC上的一动点,DE垂直AB于点E,DF垂直AC于点F.当点D运动到什么位置DE=DF说明理
如图所示,圆o的直径AB=4.角ABC=30°BC=4根号3,D是线段BC的中点!判断点D与圆o之间的位置关系 并说明理
已知等腰三角形ABC的底边长BC=20,D是AB上的点.且CD=16,AD=12,求三角形ABC的面积?
如图,在三角形ABC中,点D在边BC上,且BC=BD+AD.点D在哪条线段的垂直平分线上?
如图,AD是等腰三角形ABC的底边BC上的高,DE平行AB,交AC于点E,判断△ABC是不是等腰三角形,并说明理由
如图,在△ABC中,AB=AC D是线段AB的一个黄金分割点且 AD:AB=BD:AD 连接CD 且AD=BC,
如图,AD是等腰三角形ABC的底边BC上的高,DE平行AB,交AC于点E,判断△ADE是不是等腰三角形,并说明理由
ad是等腰三角形abc的底边bc上的高,de//ab,交ac于点e,判断三角形ade是不是等腰三角形,并说明理由
AD是等腰三角形ABC的底边BC上的高,DE‖AB,交AC于点E,判断△ADE是不是等腰三角形,并说明理由