已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是17
来源:学生作业帮 编辑:神马作文网作业帮 分类:数学作业 时间:2024/11/18 21:22:57
 已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是
已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是| 17 |
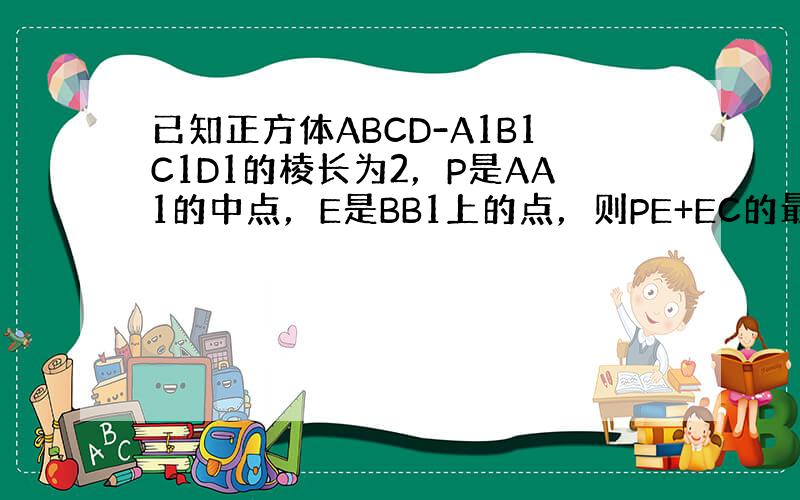
根据题意可得:可以把平面BCC1B1展开,如图所示,

若PE+EC取最小值,则P,E,C三点共线,
∴PE+EC的最小值为PC,
∵正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,
∴|PC|=
12+42=
17.
故答案为:
17.

若PE+EC取最小值,则P,E,C三点共线,
∴PE+EC的最小值为PC,
∵正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,
∴|PC|=
12+42=
17.
故答案为:
17.
(2014•南昌模拟)已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别是边AA1、CC1上的中点,点M是BB1
在棱长为1的正方体ABCD—A1B1C1D1中,E是棱BB1的中点,P是截面ABC1D1上的一动点,则A1P+PE的最小
在棱长为1的正方体ABCD-A1B1C1D1中点E,F,G分别是DD1,BD,BB1的中点
已知正方体ABCD-A1B1C1D1的棱长为1,点E、F分别是A1D1、AC的中点,求直线EF与AA1夹角的余弦.
已知正方体ABCD-A1B1C1D1中,M是AA1的中点,N是BB1的中点.求证:平面MDB1//平面ANC
在正方体ABCD-A1B1C1D1中,E,F分别是BB1,CD的中点.设AA1=2,求点F到平面A1ED1的距离
已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:⑴FC1‖平面ADE
棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点
已知ABCD-A1B1C1D1是一个棱长为1的正方体,o1是底面A1B1C1D1的中心,M是BB1上的点,
正方体ABCD-A1B1C1D1,E,F分别是AA1,CC1的中点,P是CC1上的动点(包括端点),过点E、D、P作正方
在棱长为1的正方体ABCD-A1B1C1D1中,点E,F,G分别是DD1,BD,BB1中点.求CE的长
在棱长为1的正方体ABCD--A1B1C1D1中,若G、E分别为BB1,C1D1的中点,点F是正方形ADD1A1的中心,