(2014•吴中区一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长
来源:学生作业帮 编辑:神马作文网作业帮 分类:综合作业 时间:2024/11/23 18:51:11
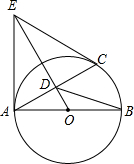 (2014•吴中区一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.
(2014•吴中区一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;
(2)连接BD,若ED:DO=3:1,OA=9,求:
①AE的长;
②tanB的值.

(1)连接OC,
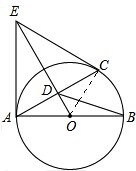
∵OD⊥AC,OC=OA,
∴∠AOD=∠COD.
在△AOE和△COE中
OA=O C
∠AOE=∠COE
OE=OE
∴Rt△AOE≌Rt△COE(SAS),
∴∠EAO=∠ECO.
又∵EC是⊙O的切线,
∴∠ECO=90°.
∴∠EAO=90°.
∴AE与⊙O相切;
(2)①设DO=t,则DE=3t,EO=4t,
∵
AO
DO=
EO
AO,即
9
t=
4t
9,
∴t=
9
2,即EO=18.
∴AE=
EO2−AO2=
182−92=9
3;
②延长BD交AE于F,过O作OG∥AE交BD于G,
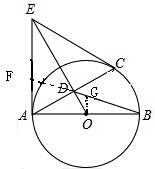
∵OG∥AE,
∴∠FED=∠GOD.
又∵∠EDF=∠ODG,
∴△OGD∽△EFD.
EF
OG=
ED
DO=
3
1,即EF=3GO.
又∵O是AB的中点,
∴AF=2GO.
∴AE=AF+FE=5GO.
∴5GO=9
3,
∴GO=
9
3
5.
∴AF=
18
3
5.
∴tanB=
AF
AB=
3
5.

∵OD⊥AC,OC=OA,
∴∠AOD=∠COD.
在△AOE和△COE中
OA=O C
∠AOE=∠COE
OE=OE
∴Rt△AOE≌Rt△COE(SAS),
∴∠EAO=∠ECO.
又∵EC是⊙O的切线,
∴∠ECO=90°.
∴∠EAO=90°.
∴AE与⊙O相切;
(2)①设DO=t,则DE=3t,EO=4t,
∵
AO
DO=
EO
AO,即
9
t=
4t
9,
∴t=
9
2,即EO=18.
∴AE=
EO2−AO2=
182−92=9
3;
②延长BD交AE于F,过O作OG∥AE交BD于G,

∵OG∥AE,
∴∠FED=∠GOD.
又∵∠EDF=∠ODG,
∴△OGD∽△EFD.
EF
OG=
ED
DO=
3
1,即EF=3GO.
又∵O是AB的中点,
∴AF=2GO.
∴AE=AF+FE=5GO.
∴5GO=9
3,
∴GO=
9
3
5.
∴AF=
18
3
5.
∴tanB=
AF
AB=
3
5.
(2014•吴中区一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长
(2013•南通一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线
已知,如图,AB是圆O的直径,C是圆O上一点,OD垂直BC于点D,过点C作圆O的切线,交OD的延长线于点E,连接BE
(2011•咸宁)如图,AB是⊙O的直径,过B点作⊙O的切线,交弦AE的延长线于点C,作OD⊥AC,垂足为D,若∠ACB
如图,AB是园O的直径,C是园O上一点,OD垂直BC于点D,过点C作园O的切线,交OD的延长线于点E,连接BE
已知:如图AB是圆O直径C是圆O上一点OD⊥BC于点D过点C作圆O的切线,交OD的延长线于点E.连结BE,连结AD并延长
如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
已知,如图,AB是圆o的直径,C是圆o上的一点,OD⊥BC,过点c作圆o的切线,交OD的延长线与E谢谢了,
如图,AB是⊙O的直径,AD与⊙O相切于点A,过B点作BC∥OD交⊙O于点C,连接OC、AC,AC交OD于点E.
如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE
(2014•长沙二模)如图,AB为⊙O的直径,OD⊥AC于D,AC交⊙O于点E,D为AC上一点,∠AOD=∠C.
(2012•阜宁县三模)如图,AB是半圆O的直径,点C是⊙O上一点(不与A,B重合),连接AC,BC,过点O作OD∥AC