∫▒1 (e^x e^(-x) ) dx
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/12 05:40:21
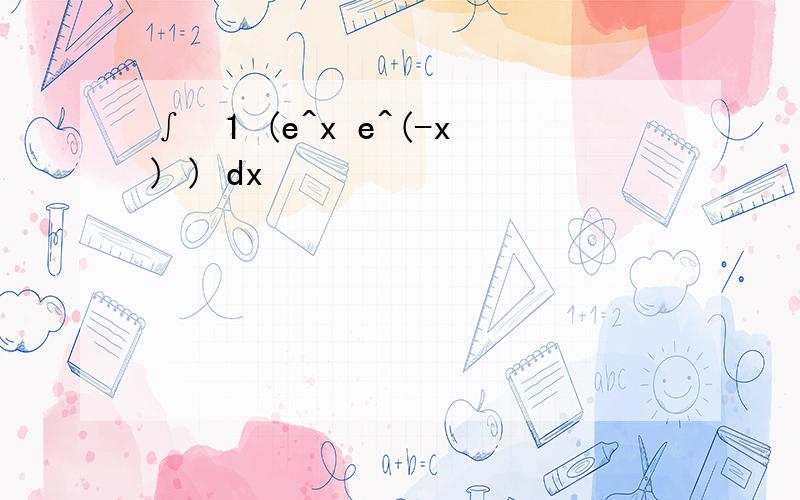
设:f(x)=e^x-ex则:f'(x)=e^x-e当x>1时,f'(x)>0即:函数f(x)在x>1时是递增的,则:对于任意x>1,都有:f(x)>f(1)=0成立,即:对一切x>1,有:e^x-e
设t=√(1+e^x),x=ln(t²-1),dx=2t/(t²-1)dt∫xe^x/√(1+e^x)dx=∫[ln(t²-1)*(t²-1)/t]*2t/(t
不定积分:1.题似乎没写对,∫e^(5t)dt=(1/5)e^(5t)+C2.(-1/2)[(2-3x)^(2/3)]+C3.-2cos√t+C4.(-1/2)e^(-x^2)+C5.(-1/4)[(
前一个式子(xe^x)'-(e^x)'=(x'e^x+xe^x)-e^x=e^x+xe^x-e^x=xe^x
看起来好高端的样子,青年人网上有名师指导,高数题就是很折磨人!
∫xe^(1/x)dx=-∫xe^(-x)d(-x)=-∫xde^(-x)=-(xe^(-x)-∫e^(-x)dx)=-xe^(-x)+∫e^(-x)dx=-xe^(-x)-∫e^(-x)d(-x)=
∫xe^(-x)dx/(1+e^(-x))^2=∫xe^xdx/(1+e^x)^2=∫xde^x/(1+e^x)^2=∫xd(-1/(1+e^x))=-x/(1+e^x)+∫dx/(1+e^x)=-x
1.令y=e^x,x=lny,dx=1/ydy.原式=∫lny/(y+1)^2dy分部积分:令u=lny,v'=1/(y+1)^2则∫lny/(y+1)^2dy=-lny/(y+1)+∫1/y(y+1
integral(e^xx)/sqrt(e^x-1)dxFortheintegrand(e^xx)/sqrt(e^x-1),substituteu=sqrt(e^x-1)anddu=e^x/(2sqr
∫(-1,1)xe^(x|x|)dx=∫(-1,0)xe^(-x^2)dx+∫(0,1)xe^x^2dx=-1/2∫(-1,0)e^(-x^2)d(-x^2)+1/2∫(0,1)e^x^2dx^2=1
令y=e^x,x=lny,dx=1/ydy.原式=∫lny/(y+1)^2dy分部积分:令u=lny,v'=1/(y+1)^2则∫lny/(y+1)^2dy=-lny/(y+1)+∫1/y(y+1)d
∫f(x)dx=xe²就是求导,因为xe²*是原函数,那么f(x)就是它的导数xe^2x`=e^2x+x*2e^2x就是e²*+2xe²*
貌似你会得不到初等函数解.
点击即可放大,哈哈!
∫xe^xdx,=∫xde^x=xe^x-∫e^xdx=xe^x-e^x+c∫e^xcos2xdx=(1/2)∫e^xdsin2x=(1/2)e^xsin2x-(1/2)∫sin2xe^xdx=(1/
我觉得你算的是对的,没什么问题.再问:我知道呀,但是无穷那个怎么带进去得到ln2呀,最后出答案的地方不会!再答:-x/(1+e^x)这项应该会吧x-ln(1+e^x)=lne^x-ln(1+e^x)=
∫xe^(x^2)/(1-2e^(x^2)dx=(-1/4)∫1/[2e^(x^2)-1]d(2e^(x^2)-1)=(-1/4)ln[2e^(x^2)-1]+C