∫(ln(1-x)) xdx
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/20 12:00:09
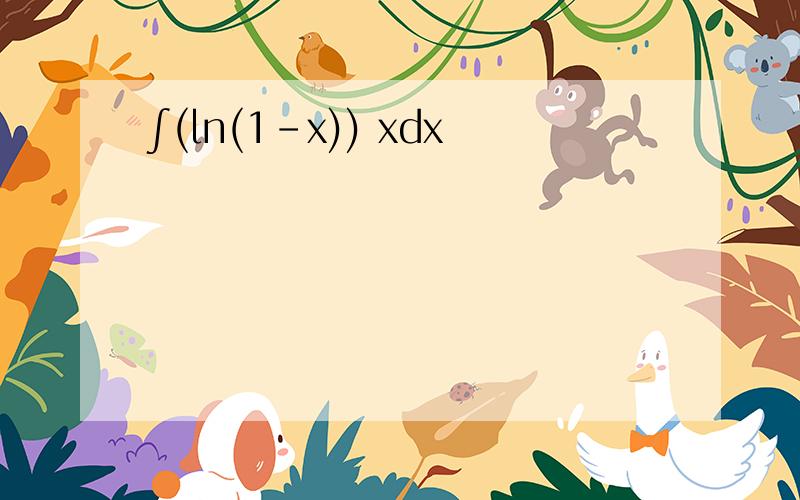
利用分部积分=xlnx-∫x*(1/x)dx=xlnx-x =-1 xlnx 在x=0处极限为0
用分部积分法就可以很快得出答案,1.∫xdx/(1+x*x*x*x)=x*x/(1+x*x*x*x)-∫x/(1+x*x*x*x)dx=x*x/(1+x*x*x*x)-1/2∫1/(1+x*x*x*x
1,xln(1+x^2)-∫2x^2/(1+x^2)dx=xln(1+x^2)-2∫(1-1/(1+x^2))dx=xln(1+x^2)-2(x-arctanx)2,设t=√x,x=t^2,dx=2t
定积分上限e下限1,xlnxdx,=∫(1,e)lnxd(x^2)/2x^2/2*lnx|(1,e)-∫(1,e)(x^2)/2dlnx=e^2/2-x^2/4|(1,e)=e^2/2-e^2/4+1
(1)令x=sint,因x属于(-1,2),故t在(-pi/2,pi/2)内,且dx=costdt∫x^2/根号(1-x^2)dx=∫(sint)^2/cost×costdt=∫(sint)^2dt=
{f(x)d(lnx)={f(e^lnx)d(lnx)=f(e^x)+c,{ln(t+1)dt={ln(t+1)d(t+1)=={e^lnt*ln(t+1)dln(t+1)={e^ln(t+1)ln(
用分步积分法就可以做出来了∫arctan1/xdx=xarctan(1/x)-∫xdarctan1/x=xarctan(1/x)-∫x/[1+(1/x)^2]*(-1/x^2)dx=xarctan(1
∫lnx/√xdx=∫lnx*2/(2√x)dx=2∫lnxd(√x)=2√xlnx-2∫√xd(lnx)、分部积分法=2√xlnx-2∫√x*1/xdx=2√xlnx-2∫1/√xdx=2√xlnx
=(1/3)∫d(3x^2-1)/√(3x^2-1)=(2/3)√(3x^2-1)+C
∫ln(1+x)/√xdx=2∫ln(1+x)/(2√x)dx=2∫ln(1+x)d√x=2ln(1+x)*√x-2∫√xdln(1+x),integrationbypart=2(√x)ln(1+x)
∫f(x)/xdx=ln[x+√(1+x²)]+Cf(x)/x=d/dx{ln[x+√(1+x²)]+C}=1/√(1+x²)f(x)=x/√(1+x²)---
用分部积分法,先把x^2放到dx里面然后分部积分再把dlnx变成1/xdx
∫x^2√xdx=∫x^(5/2)dx=2/7*x^(7/2)+C再问:∫x^(5/2)dx里的5/2怎么得出来的?再答:√x=x^(1/2)
如果有用及时采纳再问:问下为什么前面要加负号再答:加符号就对换了积分的上下限。再问:哦,谢谢
(1)原函数是F(x)=(lnx)²/2+C;所以,定积分=F(e)-F(1)=1/2-0=1/2;(2)即3x²-x-2的积分;原函数是F(x)=x³-x²/
再答:再答:第一个错了再问:不好意思,我把问题打错了,中间是除不是乘。您再看一眼,求指导!再答: