∠CBD=65° ∠BCE=25°

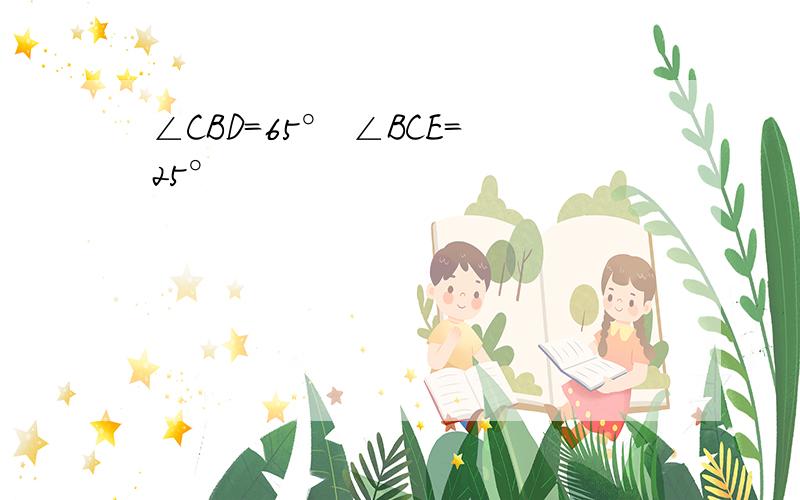
∵∠CBD、∠BCE的平分线相交于点O，∴∠OBC=12（∠A+∠ACB），∠OCB=12（∠A+∠ABC），∴∠OBC+∠OCB=12（∠A+∠ACB+∠ABC+∠A），∵∠A+∠ACB+∠ABC=

过D作DE⊥AB于E,由CD=2√3,AB=8,∴AE=8-2√3,∵sin∠A=3/5,∴cos∠A=4/5,tan∠A=3/4DE=[3×（8-2√3）]/4=（6-3√3/2）DB²=

BC不等于6吧,我算的是15/4,sincdb=5/根号下41,cos=4/根号下41,tan=5/4.

结论：AE=BD∵△ACD和△BCE都是等腰直角三角形∴AC=CD,BC=CD∵∠ACD=∠BCE=90°∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB∴△ACE≌△DCB∴AE=BD

1）∵BP平分∠CBD,∴点P到BC、BD的距离相等（角平分线上的点到这个角两边的距离相等）同理,∵CP平分∠BCE,∴点P到CB、CE的距离相等,∴点P到BD和CE（即AB、AC）的距离相等,∴点P

由题意：∠A+∠ABC+∠ACB=180°,∠OBC=1/2∠CBD=1/2(∠A+∠ACB),∠OCB=1/2∠BCE=1/2(∠A+∠ABC),又∠BOC=180°—（∠OBC+∠OCB）,所以∠

设bc=x,则x/ac=3/5,ac=5/3x,故ac^2-bc^2=ab^2得x=6即bc=6,ac=10所以bd^2=45,sin∠cbd=5分之跟下5,cos∠cbd=5分之2倍的根5tan∠c

有图可以知道）∠BFC=180°-∠FBC-∠FCB,而）∠FBC=1/2(∠BCA+∠A)）∠FCB=1/2(∠CBA+∠A)...根据外角定义.所以∠BFC=90°-1/2∠A过点F再作AD,BC

∠abd+∠acb=180-∠A=112∠dbc=180-∠cba∠ecb=180-∠bca∠dbc+∠ecb=360-∠cba-∠cba=248bf,cf为角平分线∠fbc+∠fcb=248/2=1

/>证明：过点P分别作AE、BC、AD的垂线PF、PM、PN,F、M、N为垂足,∵CP是∠BCE的平分线,∴PF=PM．∵BP是∠CBD的平分线,∴PM=PN．∴PF=PN．∴PA平分∠BAC．【此题

∠ABC=180-∠CBD=180°90°=90°，∠ACB=180°-∠A-∠ABC，=180°-30°-90°，=60°，∠BCE=180°-∠ACB，=180°-60°，=120°．答：∠BCE

已知：∠DAB+∠ABC+∠BCE=360°∵∠BAH+∠DAB=180°∠BCG+∠BCE=180°∴∠BAH+∠DAB+∠BCG+∠BCE=360°∴∠BAH+∠DAB+∠BCG+∠BCE=∠DA

CE是△ABC的高,∠BCE=45°则△BEC为等腰直角三角形所以BC=√2CE=6又BD是△ABC的高,∠CBD=30°则△BDC为直角三角形,且BD/BC=cos30°所以BD=BC*cos30°

解题思路：先用∠A表示出∠1+∠2，再根据三角形的内角和定理，即可得∠F与∠A的关系。解题过程：

证明：过点P作PO1垂直BD于点O1过点P作PO2垂直CE于点O2过点P作PO3垂直BC于点O3由BP是角CBD的平分线,得PO1=PO3由CP是角BCE的平分线,得PO2=PO3所以,PO1=PO2

（1）：∵∠ABC=60°,∠A=80°（已知）∴∠ACB=180-∠ABC-∠A=40°因为角ACB=40度所以角CBD=角ACB+角A=120度（三角形的一个外角等于与它不相邻的两个内角的和）所以

证明：过点F作FM⊥AD于M，FN⊥AE于N，FO⊥BC于O∵BF平分∠CBD，FM⊥AD，FO⊥BC，∴MF=OF，同理可得：NF=OF，∴MF=NF，又FM⊥AD，FN⊥AE，∴点F在∠DAE的角

证明：∵AB=AC，∴∠ABC=∠ACB．∵∠BCE=∠CBD，∴∠BCE-∠ACB=∠CBD-∠ABC，∴∠ACE=∠ABD．∵l∥BC，∴∠DAB=∠ABC，∠EAC=∠ACB，∴∠DAB=∠EA

证明：过点F分别作AE、BC、AD的垂线FP、FM、FN，P、M、N为垂足，∵CF是∠BCE的平分线，∴FP=FM．同理：FM=FN．∴FP=FN．∴点F在∠DAE的平分线上．

因为∠CBD=90°所以∠ABC=90°所以∠BCE=∠A+∠ABC=30+90=120°（外角定理）再问：不怎么理解,解释一下再答：因为∠CBD=90°（这是已知的）所以∠ABC=90°（因为∠CB