sin^2x ln(x √1 x^2)dx

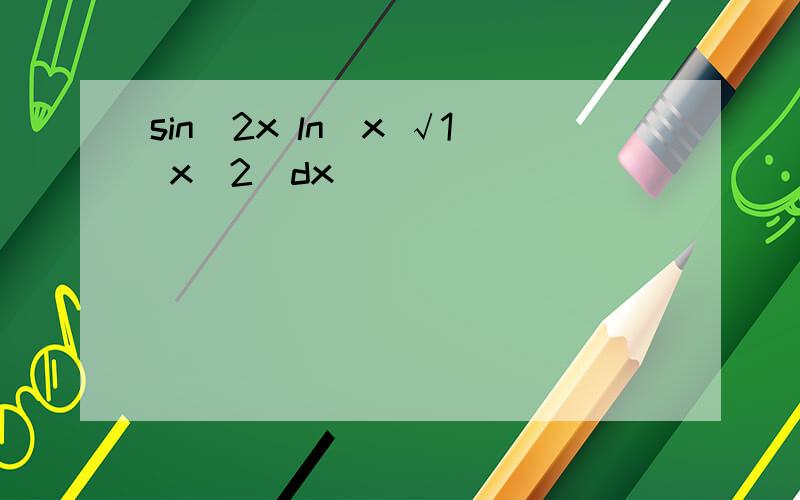
∫xln(1+x^2)dx=（1/2）∫ln(1+x^2)d(1+x^2)=(1/2)[(ln(1+x^2)(1+x^2))-(1+x^2)]

证明当x>0时,xln(x+√1+x^2)+1>√(1+x^2).【证明】设f(x)=1+xln[x+√(1+x^2)]-√（1+x^2）,x＞0,则f'(x)=ln[x+√（1+x^2)]+x[1+

∫xln(1+x^2)dx=1/2∫ln(1+x^2)dx^2=1/2∫ln(1+x^2)d(1+x^2)=1/2(1+x^2)ln(1+x^2)-1/2∫(1+x^2)dln(1+x^2)=1/2(

integral(xlog(x-1))/(x^2-1)dx=1/4(2Li_2((1-x)/2)+log(x-1)(log(x-1)+2log((x+1)/2)))+constant该积分不能用初等函

打字不便,lim下的x→+∞省略,lim[xln(x+2e^x)/ln(x+e^x)]=lim{x[x+ln(2+x/e^x)/[x+ln(1+x/e^x)]}=lim[x(x+ln2)/x]=+∞再

∫xln(1+x^2)dx=(1/2)∫ln(1+x^2)d(x^2)设x^2=u=(1/2)∫ln(1+u)du=(1/2)[uln(1+u)-∫u/(1+u)du]=(1/2)[uln(1+u)-

f(x)是g(x)的高阶无穷小.ln(1-x²)~-x²,所以f(x)~-3x³,g(x)=sin²x~x²再问：那么麻烦再问一下，这种ln(1-x&

把sin²x变成(1-cos2x)/2,把ln(2+x/2-x)变成ln(2+x)-ln(2-x),把原式拆开,ln与cos相乘的那一项用分部积分,就这样.不懂的话随时问我,我昨天刚考完研.

设f(x)=1+xln[x+√(1+x^2)]-√（1+x^2）,x＞0,则f'(x)=ln[x+√（1+x^2)]+x[1+x/√（1+x^2)]/[x+√(1+x^2)]-x/√（1+x^2)=l

利用求导公式很容易就可以证明,设f(x)=xln(x+√(1+x^2))-√(1+x^2)+1,对其求导,即可得出f'(x)=ln(x+√(1+x^2)),若x>0,那么f'(x)>0,另外可求出,f

答：∫ xln(x∧2+1)dx=(1/2) ∫ ln(x^2+1) d(x^2+1)=(1/2)*(x^2+1)*[ln(x^2+1)-1]+C再问：���˵

不懂请追问再问：1/x怎么体现出来？再答：这个是用洛必达法则，分子、分母同时求导！x求导为1不懂请追问希望能帮到你，望采纳！

这个题蛮简单的嘛你看下数学课本上的例题啊!任意x这个要分范围来界定比如：x>0;x=0;X再问：那你可以把x

题目不完整.缺x趋向?

我有一种方法,但是比较麻烦.你可以参考一下.令g(x)=xln[(1+x)/(1-x)]+cosx-1-(x^2)/2则g’(x)=ln(1+x)+x/(1+x)-ln(1-x)+x/(1-x)-si

你好!答案是-1/2.详解如图：http://hi.baidu.com/wusongsha0926/album/item/f2f445cf7bcb0a4674a290706b63f6246a60af8

定义f(x)=1+xln(x+√1+x^2)-√1+x^2则f'(x)=1+arshx注意ln(x+√1+x^2)=arshx以及(arshx)'=1/√1+x^2考虑到(arshx)'=1/√1+x

f(x)=1+xln[x+√(x^2+1)]-√(x^2+1)f'(x)=ln[x+√(x^2+1)]+x/√(x^2+1)-x/√(x^2+1)=ln[x+√(x^2+1)]f'(-x)=ln[-x

∫xln(x+√(1+x^2))dx=1/2∫ln(x+√(1+x^2))dx^2=1/2ln(x+√(1+x^2))·x^2-1/2∫x^2dln(x+√(1+x^2))=1/2*x^2*ln(x+