设p是△ABC所在平面外的一点,bc ba=2BP
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/23 19:42:30
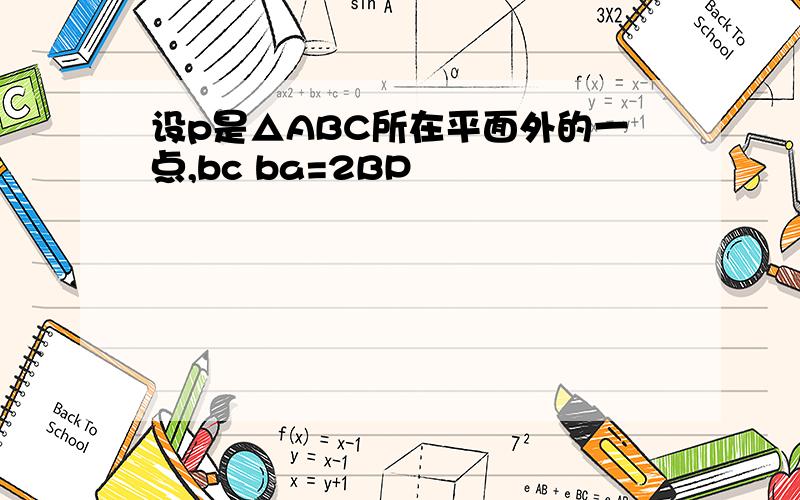
如图P是△ABC所在平面外一点,O是P点在平面a上的射影.若P到△ABC三个顶点的距离相等,由由条件可证得OA=OB=OC,由三角形外心的定义知此时点O是三角形的外心,故答案为:外;如图P是△ABC所
因为PO垂直于平面ABC,所以OA=OB=OC=根号下(PA平方-PO平方)=根号下(PB平方-PO平方)=根号下(PC平方-PO平方)所以O是三角形ABC的外心.
过C作CB’⊥PC,交PB于B'因为平面PAC⊥平面PBC所以,CB'⊥平面PAC,所以,CB'⊥PA而由PA⊥平面ABC,知PA⊥CBPA与面CBB'不垂直所以,B、B'重合即:CB⊥面PAC所以,
1)做P点在△ABC所在平面内的射影P'点,连接P'A、P'B、P'CPP'⊥面ABC,又PA=PB=PC由三垂线定理可得P'A=P'B=P'C点P在△ABC所在平面内的射影P'是△ABC的外心.2)
PA垂直面ABC所以PA垂直BC圆内AB为直径,所以AC垂直BCPA与AC相交于A所以BC垂直面PAC因为BC属于面PBC所以面PAC垂直面PBC
因为H是三角形ABC的垂心,连接AH,所以AH垂直BC.又因为PA垂直PB,PA垂直PC,所以PA垂直平面PBC,所以PA垂直BC.那么就可以知道BC垂直于平面PAH.PH又在平面PAH内,所以BC垂
证明:如答图所示,取BC的中点D,连接PD、AD,∵D是直角三角形ABC的斜边BC的中点∴BD=CD=AD,又PA=PB=PC,PD是公共边∴∠PDA=∠PDB=∠PDC=90°∴PD⊥BC,PD⊥D
连接AM并延长交BC于M1,连接AN并延长交CD于N1,连接M1N1.因为M、N分别是ABC、ACD的重心,所以AM:AM1=2:3,AN:AN1=2:3,因此MN//M1N1,而M1N1在平面BCD
证明:过点P作PQ⊥面ABC则Q点即为P点在面ABC上的射影∵PA=PB=PC∴根据三垂线定理得:AQ=BQ=CQ故Q是三角形ABC得中心∵∠BCA=90°∴Q点必为BC边的中点∵PQ∈面ABC∴根据
作两条边的垂直平分线,两线交于一点,过此点作三角型所在的平面的垂线,所得线上平面外的点均是所求点.
分析:过P作PQ⊥面ABC于Q,则Q为P在面ABC的投影,因为P到A,B,C的距离相等,所以有QA=QB=QC,即Q为三角形ABC的外心,Q到三角形ABC各边的距离相等,即Q为三角形ABC的外心,所以
过P作PQ⊥面ABC于Q,则Q为P在面ABC的投影,因为P到A,B,C的距离相等,所以有QA=QB=QC,即Q为三角形ABC的中心,因为角BAC为直,所以Q在线段BC上,所以在面PCB上有线段PQ⊥平
证明:∵PA⊥ABC∴平面PAC⊥平面ABC,且两平面交线为AC又∵平面PAC⊥平面PBC,且平面平面PBC与平面ABC的交线为BC∴BC⊥平面PAC∵AC在平面PAC上∴BC⊥AC
证明:设O是P点在平面a上的射影,连结AO并延长,交BC与D连结BO并延长,交AC与E;因PA⊥PB,PA⊥PC,故PA⊥面PBC,故PA⊥BC;因PO⊥面ABC,故PO⊥BC,故BC⊥面PAO,故A
MS是10个··一个是三角形的中心··三个是在△三条边上做三个等边△··在AC的中垂线上做BP=AC,可以上面一个下面一个这样一条边有2个三边有6个
因为O是斜边AC的中点,所以OA=OB=OC,又因为PA=PB=PC,PO是公共边,所以△POA,△POB,△POC都全等,所以角POA,POB,POC都相等,都等于90度亦即PO⊥OA,PO⊥OB所
证俩平面平行,只需证两平面内不共线的两条直线分别平行延长PA1交平面ABC于M,延长PB1交平面ABC于N,延长PC1交平面ABC于Q.连接A1B1,MN,A1C1,MQ因为A1,B1,C1是重心,所
证明:延长BH交AC于F,延长CH交AB于E,∵PB⊥PA,PB⊥PC,∴PB⊥平面PAC,∵BF⊥AC,∴PF⊥AC,∴CA⊥平面PFB,∵PH⊂平面PFB,∴PH⊥AC,同理可证PH⊥AB,∵AC
过P作面ABC的垂线,垂足为O,连接OA,OB,OC,OP则OA=sqrt(PA^2-PO^2)OB=sqrt(PB^2-PO^2)OC=sqrt(PC^2-PO^2)∵PA=PB=PC∴OA=OB=
1.中心此为正三角形2.垂心PA⊥BC,则OA⊥BC,OA是BC的高3.内心O到3边距离相等,O为内接圆圆心4.重心这个解释起来太麻烦了,你可以理解为O点是支撑起三角形的最佳力点,证明你还是回去问问老