lim√ ̄(1 tanx)
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/11 18:07:19
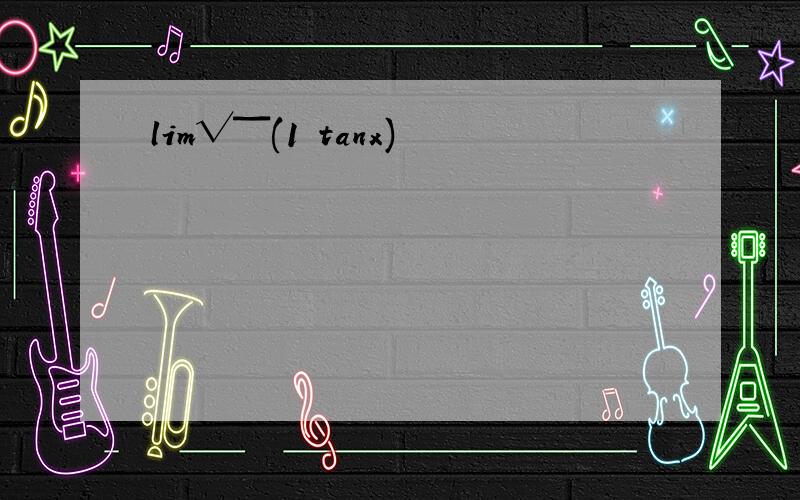
lim(1/x)^tanx根据等价无穷小简化成lim(1/x)^x【x→0+】=lim1/x^x对x^x取对数lnx^x,得xlnx,化成lnx/[1/x]洛必达法则:上下求导,分子1/x分母-1/x
分子有理化lim(x→0)[√(1+tanx)-√(1-tanx)]/sinx=lim(x→0)[√(1+tanx)-√(1-tanx)][√(1+tanx)+√(1-tanx)]/{sinx[√(1
tanx-x在x趋向0是这个整体趋向0把tanx-x看作是t的话e^(tanx-x)-1=e^(t)-1=t分母也是t,那么答案就是1了用罗比他法则的话,上下求一次导进行了分子等于e^(tanx-x)
答案为1,我给你说思路,对1/√x取e为底的指数,不明白可追问
lim(x→0)[√(1+tanx)-√(1+sinx)]/[x*ln(1+x)-x^2]=lim(x→0)[tanx-sinx]/[x*ln(1+x)-x^2][√(1+tanx)+√(1+sinx
lim√(1-cosx)/tanx=lim-√2sin(x/2)/tanx=lim-√2/2x/x=-√2/2lim√(1-cosx)/tanx=lim√2sin(x/2)/tanx=lim√2/2x
先上下通分,同乘√(1+tanx)+√(1+sinx)得Lim(tanx-sinx)/2[x(√(1+sin²x)-1)]{其中,lim√(1+tanx)+√(1+sinx)=2}=lim(
lim(tanx-sinx)/x(x→0)=limsec^2x-cosx)(x→0)=1-1=0lim(1-cos4x)/xsinx(x→0)=lim(1/2)*16x^2/x^2(x→0)=8再问:
再问:√1+x2-1怎么代成1/2x2的??再问:求解这步,看不懂。。再问:谢谢你,现在明白了
lim(x->0)[√(1+tanx)-√(1+sinx)]/[x√(1+sin²x)-x]=lim[√(1+tanx)-√(1+sinx)]*[√(1+tanx)+√(1+sinx)]/[
lim(x→0)[√(1+tanx)-√(1+sinx)]/x分子分母同时乘以[√(1+tanx)+√(1+sinx)]=lim(x→0)[√(1+tanx)-√(1+sinx)]*[√(1+tanx
1,lim(x->1)(1-x)tanπ/2lim12x/12*1tbanπ*1/3x2,lim(x->0)(tanx-sinx)/x^3lim20x2xtansixn/30x
原式=lim{x->0}{tan(sinx)-tan(tanx)[1+cos(tanx)-1]}/(tanx-sinx)=lim{x->0}{tan(sinx-tanx)[1+tan(sinx)tan
(1)lim(x->0)[√(1-cos(x²))/(1-cosx)]=lim(x->0)[√(2sin²(x²/2))/(2sin²(x/2))](应用半角公
x→0lim[(1+tanx)^cotx]=x→0lim[(1+tanx)^(1/tanx)]=e
你好!答案是-1/2.详解如图:http://hi.baidu.com/wusongsha0926/album/item/f2f445cf7bcb0a4674a290706b63f6246a60af8
底数和指数分开求:底数:limtanx-x/x-sinx(0/0形式,求导)=lim1/cos^2(x)-1/1-cosx(0/0形式,再求导)=lim2sinx/cos^3(x)/sinx=2/si
应该是∞无穷大分子cos√(1-x^2)趋近于cos1分母tanx趋近于0ln(1+x)趋近于0实数除以一个无穷小应该就是无穷大咯